
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.
(1)求证:△AOC≌△CEB;
(2)求△ABD的面积.

【答案】(1)详见解析;(2)6.
【解析】
(1)根据等腰直角三角形的性质,可得AC=BC,∠ACB=90°,根据余角的性质,可得∠OAC=∠BCE,根据AAS,可得答案;
(2)根据全等三角形的性质,可得B点坐标,根据待定系数法,可得b的值,根据三角形的面积公式,可得答案.
(1)证明:∵BE⊥CE,
∴∠BEC=90°,
∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∵∠O=∠ACB=90°,
∴∠OAC+∠ACO=90°,∠ACO+∠BCE=90°,
∴∠OAC=∠BCE,
在Rt△AOC和Rt△CEB中,
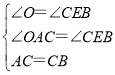 ,
,
∴Rt△AOC≌Rt△CEB(AAS);
(2)如图:作BF⊥y轴于F点,
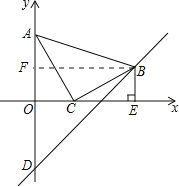
∵Rt△AOC≌Rt△CEB,
∴CE=OA=2,BE=OC=1,
∴OE=CC+CE=1+2=3,
即B(3,1),BF=3,
将B点坐标代入y=x+b,得3+b=1,
解得b=-2,
直线BD的解析式为y=x-2,
当x=0时,y=-2,即D(0,-2),
S△ABD=![]() ADBF=
ADBF=![]() ×[2-(-2)]×3=6.
×[2-(-2)]×3=6.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.
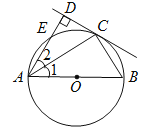
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.

(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
(1)求直线BC的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
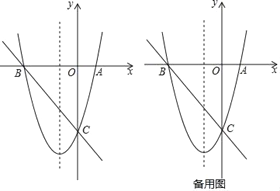
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①为Rt△AOB,∠AOB=90°,其中OA=3,OB=4.将AOB沿x轴依次以A,B,O为旋转中心顺时针旋转.分别得图②,图③,…,则旋转到图⑩时直角顶点的坐标是_____.
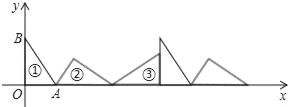
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列因式分解的过程,再回答所提出的问题:
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]
=(1+x)2(1+x)
=(1+x)3
(1)上述分解因式的方法是 ,共应用了 次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,则需应用上述方法 次,结果是 .
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+ x(x+1)n(n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格如表:
购票人数/人 | 1~50 | 51~100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
 A、2
A、2
B、4
C、![]()
D、![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com