
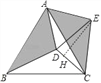
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E.
(1)DE=_____;
(2)∠CDE的正切值为_____.

【答案】 5, 3![]()
【解析】分析:(1)先利用等边三角形的性质AB=AC,∠BAC=60°,再根据旋转的性质得AD=AE, ∠DAE=∠BAC=60°,CE=BD=6,然后判断△ADE为等边三角形得到DE的长;(2) 作EH⊥CD于H, 设DH=x,则CH=4﹣x,利用勾股定理得到52﹣x2=62﹣(4-x),解得x=![]() ,再计算出EH的长,然后利用正切的定义求解.
,再计算出EH的长,然后利用正切的定义求解.
详解:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,
∴AD=AE,∠DAE=∠BAC=60°,CE=BD=6,
∴△ADE为等边三角形,
∴DE=AD=5;
(2)作EH⊥CD于H,如图,
设DH=x,则CH=4﹣x,
在Rt△EDH中,EH2=DE2﹣DH2=52﹣x2,
在Rt△ECH中,EH2=CE2﹣CH2=62﹣(4﹣x)2,
∴52﹣x2=62﹣(4﹣x)2,解得x=![]() ,
,
∴EH=![]() =
=![]() ,
,
∴tan∠EDH=![]() =3
=3![]() ,
,
即∠CDE的正切值为3![]() .
.
故答案为5,3![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
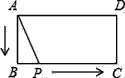
A. 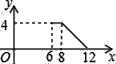 B.
B. 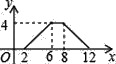 C.
C. 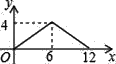 D.
D. 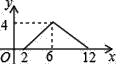
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.

(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB为⊙O的直径,AD平分∠CAB,AC⊥CD,垂足为C.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)求证:∠CDA=∠AED.

查看答案和解析>>
科目:初中数学 来源: 题型:
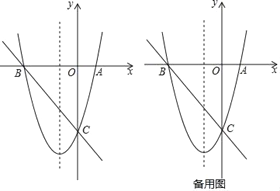
【题目】如图,已知抛物线y=![]() x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
(1)求直线BC的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
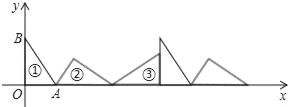
【题目】如图①为Rt△AOB,∠AOB=90°,其中OA=3,OB=4.将AOB沿x轴依次以A,B,O为旋转中心顺时针旋转.分别得图②,图③,…,则旋转到图⑩时直角顶点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列因式分解的过程,再回答所提出的问题:
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]
=(1+x)2(1+x)
=(1+x)3
(1)上述分解因式的方法是 ,共应用了 次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,则需应用上述方法 次,结果是 .
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+ x(x+1)n(n为正整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com