
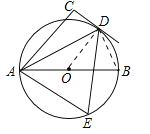
【题目】如图所示,AB为⊙O的直径,AD平分∠CAB,AC⊥CD,垂足为C.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)求证:∠CDA=∠AED.

【答案】(1)证明见解析;(2)见解析
【解析】试题分析:(1)连接OD,根据OA=OD,推出∠OAD=∠CAD,求出∠ODA=∠CAD,求出OD⊥CD,根据切线的判定推出即可;
(2)连接BD,利用AB为直径的性质进行解答.
试题解析:证明:(1)CD是⊙O的切线.证明如下:
连接OD.∵OA=OD,∴∠ODA=∠OAD.∵AD平分∠CAB,∴∠OAD=∠CAD,∴∠ODA=∠CAD.∵AC⊥CD,即∠CAD+∠CDA=90°,∴∠ODA+∠CDA=90°,∴OD⊥CD,即CD是⊙O的切线;
(2)连接BD.∵AB为直径,∴∠ADB=90°,∴∠B+∠BAD=90°,∠B=∠AED,∴∠AED+∠BAD=90°.∵∠CDA+∠CAD=90°,∠CAD=∠BAD,∴∠CDA=∠AED.


科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题
分母中含有未知数的不等式叫做分式不等式,如:![]() ;
;![]() 等
等![]() 那么如何求出它们的解集呢?
那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负![]() 其字母表达式为:
其字母表达式为:
![]() 若
若![]() ,
,![]() ,则
,则![]() ;若
;若![]() ,
,![]() ,则
,则![]()
![]() 若
若![]() ,
,![]() ,则
,则![]() ;若
;若![]() ,
,![]() ,则
,则![]()
反之:![]() 若
若![]() ,则
,则![]() 或
或![]()
![]() 若
若![]() ,则______或______.
,则______或______.
根据上述规律
![]() 求不等式
求不等式![]() 的解集.
的解集.
![]() 直接写出一个解集为
直接写出一个解集为![]() 或
或![]() 的最简分式不等式.
的最简分式不等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米.
(1)这个云梯的底端B离墙多远?
(2)如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠A=90°,AC=12,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转90°得到线段OD,要使点D恰好落在BC边上,则OP的长等于( )
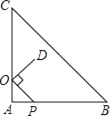
A. 5 B. 3![]() C. 3
C. 3![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在坐标平面内△ABC的顶点坐标分别为A(0,2),B(3,3),C(2,1),(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC关于原点对称的△A1B1C1,并直接写出点C1点的坐标;
(2)画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E.
(1)DE=_____;
(2)∠CDE的正切值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
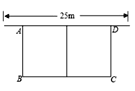
【题目】如图,有长为48米的篱笆,一面利用墙(墙的最大可用长度25米),围成中间隔有一道篱笆的长方形花圃ABCD.
(1)当AB的长是多少米时,围成长方形花圃ABCD的面积为180![]() ?
?
(2)能围成总面积为240![]() 的长方形花圃吗?说明理由.
的长方形花圃吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 的表达式为
的表达式为![]() ,点A,B的坐标分别为
,点A,B的坐标分别为
(1,0),(0,2),直线AB与直线![]() 相交于点P.
相交于点P.
(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线![]() 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com