

分析 (1)根据题意得出BO的长,再利用路程除以速度得出时间;
(2)根据切线的性质和判定结合等腰直角三角形的性质得出AO的长,进而求出答案;
(3)利用圆周角定理以及切线的性质定理得出∠CEF=∠ODF=∠OFD=∠CFG,进而求出△CFG∽△CEF,即可得出答案.
解答 (1)解:由题意可得:BO=4cm,t=$\frac{4}{2}$=2(s);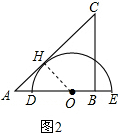
(2)解:如图2,连接O与切点H,则OH⊥AC,
又∵∠A=45°,
∴AO=$\sqrt{2}$OH=3$\sqrt{2}$cm,
∴AD=AO-DO=(3$\sqrt{2}$-3)cm;
(3)证明:如图3,连接EF,
∵OD=OF,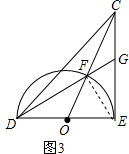
∴∠ODF=∠OFD,
∵DE为直径,
∴∠ODF+∠DEF=90°,
∠DEC=∠DEF+∠CEF=90°,
∴∠CEF=∠ODF=∠OFD=∠CFG,
又∵∠FCG=∠ECF,
∴△CFG∽△CEF,
∴$\frac{CF}{CG}$=$\frac{CE}{CF}$,
∴CF2=CG•CE.
点评 此题主要考查了切线的性质以及相似三角形的判定与性质、等腰直角三角形的性质等知识,根据题意得出△CFG∽△CEF是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
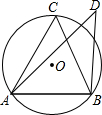 如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:
阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:| 个数分组 | 28≤x<36 | 36≤x<44 | 44≤x<52 | 52≤x<60 | 60≤x<68 |
| 频数 | 2 | 5 | 7 | 4 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{17}{24}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $(\frac{1}{2})^{0}$=1 | B. | x2+x2=2x4 | C. | |a|=|-a| | D. | $(\frac{b}{{a}^{2}})^{3}$=$\frac{{b}^{3}}{{a}^{6}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com