
分析 (1)直接利用二次函数的定义得出a2+1=2,a+1≠0得出即可;
(2)利用一次函数的定义分别求出即可.
解答 解:(1)当$\left\{\begin{array}{l}{{a}^{2}+1=2}\\{a+1≠0}\end{array}\right.$时,函数为二次函数,
解得:a=1;
(2)当$\left\{\begin{array}{l}{{a}^{2}+1=1}\\{a+1+a-2≠0}\end{array}\right.$时,函数为一次函数,
解得:a=0,
当a+1=0,即a=-1时,函数为一次函数,
所以,当函数为二次函数时,a=1,当函数为一次函数时,a=0或-1.
点评 此题主要考查了二次函数与一次函数的定义,正确把握相关定义是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一块两边长分别为AB=6m,BC=8m的长方形草地上,顶点A、B、C、D处各居住着一只蚂蚁,居住在顶点A处的蚂蚁准备拜访居住在C点的蚂蚁,它到达C点的行程最少为( )
如图,在一块两边长分别为AB=6m,BC=8m的长方形草地上,顶点A、B、C、D处各居住着一只蚂蚁,居住在顶点A处的蚂蚁准备拜访居住在C点的蚂蚁,它到达C点的行程最少为( )| A. | 7m | B. | 8m | C. | 9m | D. | 10m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
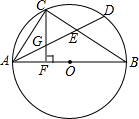 如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG.
如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
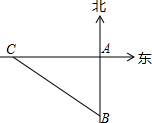 如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.
如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com