
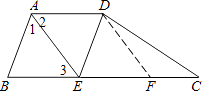
【题目】如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE. 
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°,CE=2BE,试判断△CDE的形状,并说明理由.
【答案】
(1)证明:如图,∵AE平分∠BAD,
∴∠1=∠2,
∵AB=AD,AE=AE,
∴△BAE≌△DAE,
∴BE=DE,
∵AD∥BC,
∴∠2=∠3=∠1,
∴AB=BE,
∴AB=BE=DE=AD,
∴四边形ABED是菱形.
(2)解:△CDE是直角三角形.
如图,过点D作DF∥AE交BC于点F,
∵AD∥BC,DF∥AE
∴四边形AEFD是平行四边形,
∴DF=AE,AD=EF=BE,
∵CE=2BE,
∴BE=EF=FC,
∴DE=EF,
又∵∠ABC=60°,AB∥DE,
∴∠DEF=60°,
∴△DEF是等边三角形,
∴DF=EF=FC,
∴△CDE是直角三角形.
【解析】(1)根据AB=AD及AE为∠BAD的平分线可得出∠1=∠2,从而证得△BAE≌△DAE,这样就得出四边形ABED为平行四边形,根据菱形的判定定理即可得出结论;(2)过点D作DF∥AE交BC于点F,可得出DF=AE,AD=EF=BE,再由CE=2BE得出DE=EF,从而结合∠ABC=60°,AB∥DE可判断出结论.
【考点精析】解答此题的关键在于理解梯形的定义的相关知识,掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈ ![]() ,cos67°≈
,cos67°≈ ![]() ,tan67°≈
,tan67°≈ ![]() ,
, ![]() ≈1.73)
≈1.73)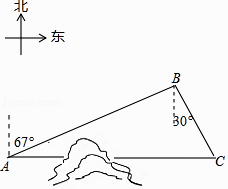
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.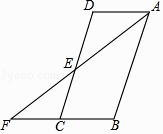
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AB= ![]() ,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( ) 
A.![]()
B.![]()
C.1
D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则BG的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( ) 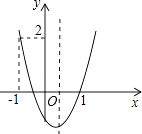
A.①⑤
B.①②⑤
C.②⑤
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+4x+m(m为常数)经过点(0,4)
(1)求m的值;
(2)将该抛物线先向右、再向下平移得到另一条抛物线.已知这条平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为l1)关于y轴对称;它所对应的函数的最小值为﹣8.
①试求平移后的抛物线所对应的函数关系式;
②试问在平移后的抛物线上是否存在着点P,使得以3为半径的⊙P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被⊙P所截得的弦AB的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为 . 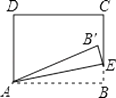
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则下列结论中错误的是( ) 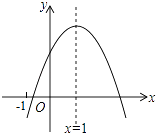
A.abc<0
B.a﹣b+c<0
C.b2﹣4ac>0
D.3a+c>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com