

| A. | 5 | B. | 20 | C. | 25 | D. | 18 |
分析 根据运算规则进行重复计算,从中发现循环的规律,得到答案.
解答 解:根据题意,得
当n=2015时,第1次的计算结果是3n+5=6050;
第2次的计算结果是$\frac{6050}{2}$=3025;
第3次的计算结果是3025×3+5=9080;
第4次是计算结果是$\frac{9080}{{2}^{3}}$=1135;
第5次的计算结果是1135×3+5=3410;
第6次的计算结果是$\frac{3410}{2}$=1705,
第7次的计算结果是1705×3+5=5120,
第8次的计算结果是$\frac{5120}{{2}^{10}}$=5,
第9次的计算结果是5×3+5=20,
第10次的计算结果是$\frac{20}{{2}^{2}}$=5,开始循环.
故第2015次的计算结果是20
故选:B.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律即可求出结果.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
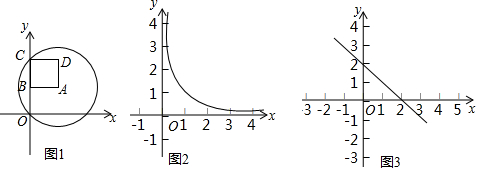
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
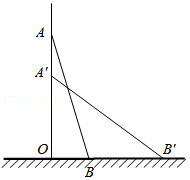 一架方梯AB长2.5米,如图,斜靠在一面墙上,梯子底端离墙OB为0.7米,
一架方梯AB长2.5米,如图,斜靠在一面墙上,梯子底端离墙OB为0.7米,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )| A. | 130° | B. | 120° | C. | 125° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知圆内接四边形ABCD,AD是⊙O的直径,OC⊥BD于E.
如图,已知圆内接四边形ABCD,AD是⊙O的直径,OC⊥BD于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com