
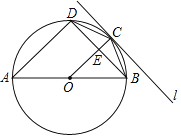
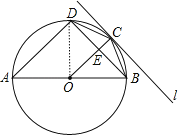
【题目】如图,AB为⊙O的直径,点C为AB上方的圆上一动点,过点C作⊙O的切线l,过点A作直线l的垂线AD,交⊙O于点D,连接OC,CD,BC,BD,且BD与OC交于点 E.
(1)求证:△CDE≌△CBE;
(2)若AB=6,填空:
①当![]() 的长度是 时,△OBE是等腰三角形;
的长度是 时,△OBE是等腰三角形;
②当BC= 时,四边形OADC为菱形.
【答案】(1)见解析;(2)①![]() π;②3
π;②3
【解析】
(1)由已知可得CE⊥BD,则可知DE=BE,所以△CDE≌△CBE(SAS);
(2)①连接OD,由已知可证明△ABD是等腰直角三角形,求得∠COD=45°,即可求![]() 的长度;②由已知可得OA=OC=AD=CD=3,再由△CDE≌△CBE,则CD=BC.
的长度;②由已知可得OA=OC=AD=CD=3,再由△CDE≌△CBE,则CD=BC.
解:(1)∵过点C作⊙O的切线l,
∴OC⊥l,
∵AD⊥l,
∴OC∥AD,
∵AB为⊙O的直径,点C为AB上方的圆上一动点,
∴AD⊥BD,
∴BD⊥OC,
∴DE=BE,
∴△CDE≌△CBE(SAS);
(2)①连接OD,
当△OBE是等腰三角形时,
∵BE⊥OE,
∴OE=BE,
∴∠OBE=∠EOB=45°,
∵AD∥OC,
∴∠A=45°,
∴△ABD是等腰直角三角形,
∴∠COD=45°,
∵AB=6,
∴AO=3,
∴![]() 的长度=
的长度=![]() =
=![]() π,
π,
故答案为![]() π;
π;
②∵四边形OADC为菱形,
∴OA=OC=AD=CD=3,
∵△CDE≌△CBE,
∴CD=BC,
∴BC=3,
故答案为3.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
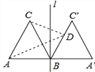
【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
A. 4 B. 3![]() C. 2
C. 2![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题时,我们常常从特殊入手,猜想结论,并尝试发现解决问题的策略与方法.
(问题提出)
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形的对边的平方和是一个定值.
(从特殊入手)
我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.
请你在图①中补全特殊殊位置时的图形,并借助于所画图形探究问题的结论.

(问题解决)
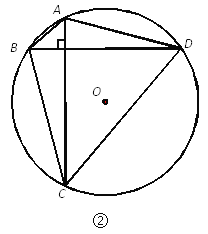
已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证: .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
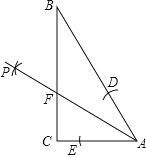
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,AC=![]() .按以下步骤作图:
.按以下步骤作图:
①以A为圆心,以小于AC长为半径画弧,分别交AC、AB于点E、D;
②分别以D、E为圆心,以大于![]() DE长为半径画弧,两弧相交于点P;
DE长为半径画弧,两弧相交于点P;
③连接AP交BC于点F.
那么BF的长为( )
A.![]() B.3C.2D.
B.3C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx﹣3与直线y=x+3交于点A(m,0)和点B(2,n),与y轴交于点C.
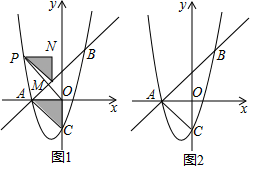
(1)求m,n的值及抛物线的解析式;
(2)在图1中,把△AOC平移,始终保持点A的对应点P在抛物线上,点C,O的对应点分别为M,N,连接OP,若点M恰好在直线y=x+3上,求线段OP的长度;
(3)如图2,在抛物线上是否存在点Q(不与点C重合),使△QAB和△ABC的面积相等?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则![]() 的长为多少?
的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
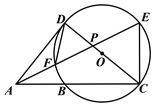
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com