练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（ ）

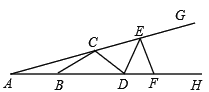
    A. 80° B. 90° C. 100° D. 108°

    【答案】B

    【解析】

    根据等腰三角形性质和三角形内角和为180°逐步算出答案．

    解：∵AB=BC，

    ∴∠ACB=∠A=18°，

    ∴∠CBD=∠A+∠ACB=36°，

    ∵BC=CD，

    ∴∠CDB=∠CBD=36°，

    ∴∠DCE=∠A+∠CDA=18°+36°=54°，

    ∵CD=DE，

    ∴∠CED=∠DCE=54°，

    ∴∠EDF=∠A+∠AED=18°+54°=72°，

    ∵DE=EF，

    ∴∠EFD=∠EDF=72°，

    ∴∠GEF=∠A+∠AFE=18°+72°=90°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】试验与探究：我们知道分数写为小数即，反之，无限循环小数写成分数即．一般地，任何一个无限循环小数都可以写成分数形式．现在就以为例进行讨论：设＝x，由＝0.7777…，可知，10x﹣x＝7.77…﹣0.777…＝7，即10x﹣x＝7，解方程得，于是得＝．

    请仿照上述例题完成下列各题：

    (1)请你把无限循环小数写成分数，即＝_____．

    (2)你能化无限循环小数为分数吗？请仿照上述例子求解之．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，转盘被等分成6个扇形，每个扇形上依次标有数字1，2，3，4，5，6．在游戏中特别规定：当指针指向边界时，重新转动转盘．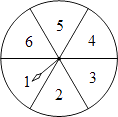
    （1）自由转动转盘，当它停止转动时，指针指向的数大于4的概率为；
    （2）请用画树状图法或列表法等方式求出“两次转动转盘，指针指向的数都大于4”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司开发出一种高科技电子节能产品，投资2500万元一次性购买整套生产设备，此外生产每件产品需成本20元，每年还需投入500万广告费，按规定该产品的售价不得低于30元/件且不得高于70元/件，该产品的年销售量y（万件）与售价x（元/件）之间的函数关系如下表：

    x（元/件）

    30

    31

    …

    70

    y（万件）

    120

    119

    …

    80


    （1）求y与x的函数关系式，并写出x的取值范围；
    （2）第一年公司是盈利还是亏损？冰球出当盈利最大或亏损最小时该产品的售价；
    （3）在（2）的前提下，即在第一年盈利最大或亏损最小时，第二年公司重新确定产品定价，能否使两年盈利3500万元？若能，求第二年产品的售价；若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，D是等边三角形ABC内一点，将线段AD绕点A顺时针旋转60°，得到线段AE，连接CD，BE．

    （1）求证：∠AEB=∠ADC；

    （2）连接DE，若∠ADC=105°，求∠BED的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC=11，∠BAC=120°，AD是△ABC的中线，AE是∠BAD的角平分线，DF∥AB交AE的延长线于点E，则DF的长为（ ）

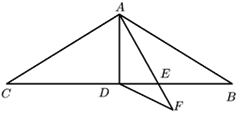
    A. 4.5 B. 5 C. 5.5 D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，AE⊥BC于点E点，延长BC至F点使CF=BE，连接AF，DE，DF．
    （1）求证：四边形AEFD是矩形；
    （2）若AB=6，DE=8，BF=10，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用白铁皮做罐头盒，每张铁皮可做盒身25个，或做盒底40个，一个盒身与两个盒底配成一套罐头盒．现有36张白铁皮，用多少张制盒身，多少张制盒底可以使盒身与盒底正好配套？

    ①设用x张制盒身，可得方程2×25x＝40(36﹣x)；

    ②设用x张制盒身，可得方程25x＝2×40(36﹣x)；

    ③设用x张制盒身，y张制盒底，可得方程组；

    ④设用x张制盒身，y张制盒底，可得方程组；其中正确的是( )

    A. ①④ B. ②③ C. ②④ D. ①③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校组织340名师生进行长途考察活动，带有行李170件，计划租用甲、乙两种型号的汽车共10辆．经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李．

    （1）请你帮助学校设计所有可行的租车方案.

    （2）如果甲车的租金为每辆2 000元，乙车的租金为每辆1 800元，问哪种可行方案使租车费用最省？

    查看答案和解析>>

    同步练习册答案