
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果: ①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,
则正确的结论是( )
A.①②③④
B.②④⑤
C.②③④
D.①④⑤
【答案】D
【解析】解:∵抛物线与x轴有两个交点,∴△=b2﹣4ac>0,即b2>4ac,故①正确; ∵抛物线对称轴为x=﹣ ![]() <0,与y轴交于负半轴,∴ab>0,c<0,abc<0,故②错误;
<0,与y轴交于负半轴,∴ab>0,c<0,abc<0,故②错误;
∵抛物线对称轴为x=﹣ ![]() =﹣1,∴2a﹣b=0,故③错误;
=﹣1,∴2a﹣b=0,故③错误;
∵当x=1时,y>0,即a+b+c>0,故④正确;
∵当x=﹣1时,y<0,即a﹣b+c<0,故⑤正确;
正确的是①④⑤.
故选D.
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


科目:初中数学 来源: 题型:
【题目】如图,这是一个供滑板爱好者使用的U型池,该U型池可以看成是一个长方体去掉一个“半圆柱”,中间可供滑行部分的截面是半径为4 m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=2 m.一滑板爱好者从A点滑到E点,则他滑行的最短路程约为____________(边缘部分的厚度忽略不计,结果保留整数.提示:482≈222).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,后解答:![]()
像上述解题过程中,![]() 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)![]() 的有理化因式是________;
的有理化因式是________;![]() 的有理化因式是________.
的有理化因式是________.
(2)将下列式子进行分母有理化:①![]() ________;②
________;②![]() ________.
________.
(3)计算![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A. 
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题的个数( )
(1)已知直角三角形面积为4,两直角边的比为1:2,则它的斜边为5;
(2)直角三角形的最大边长为26,最短边长为10,则另一边长为24;
(3)在直角三角形中,两条直角边长为n2﹣1和2n,则斜边长为n2+1;
(4)等腰三角形面积为12,底边上的底为4,则腰长为5.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1 , L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图2,已知抛物线L3:y=2x2﹣8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x﹣m)2+n的任意一条友好抛物线的解析式为y=a2 (x﹣h)2+k,请写出a1与a2的关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
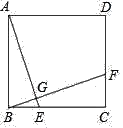
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com