
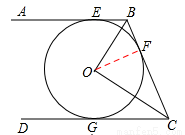
如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm.
(1)求证:BO⊥CO;
(2)求BE和CG的长.

(1)证明见解析;(2)6.4cm.
【解析】
试题分析:(1)由AB∥CD得出∠ABC+∠BCD=180°,根据切线长定理得出OB、OC平分∠EBF和∠BCG,也就得出了∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°.从而证得∠BOC是个直角,从而得出BO⊥CO;
(2)根据勾股定理求得AB=10cm,根据RT△BOF∽RT△BCO得出BF=3.6cm,根据切线长定理得出BE=BF=3.6cm,CG=CF,从而求得BE和CG的长.
试题解析:【解析】
(1)证明:∵AB∥CD,∴∠ABC+∠BCD=180°.
∵AB、BC、CD分别与⊙O相切于E、F、G,∴BO平分∠ABC,CO平分∠DCB.
∴∠OBC=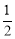 ∠ABC,∠OCB=
∠ABC,∠OCB=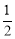 ∠DCB.
∠DCB.
∴∠OBC+∠OCB=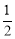 (∠ABC+∠DCB)=
(∠ABC+∠DCB)=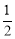 ×180°=90°.
×180°=90°.
∴∠BOC=90°. ∴BO⊥CO.
(2)如答图,连接OF,则OF⊥BC,
∴Rt△BOF∽Rt△BCO. ∴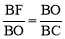 .
.
∵在RT△BOF中,BO=6cm,CO=8cm,
∴根据勾股定理得,BC=10cm,
∴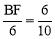 . ∴BF=3.6cm,
. ∴BF=3.6cm,
∵AB、BC、CD分别与⊙O相切,∴BE=BF=3.6cm,CG=CF.
∵CF=BC﹣BF=10﹣3.6=6.4cm,∴CG=CF=6.4cm.
考点:1.切线的性质;2. 切线长定理;3.三角形内角和定理;4.相似三角形的判定和性质;5.勾股定理.


科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:填空题
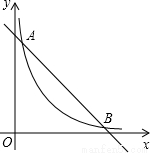
在平面直角坐标系xOy中,一次函数 的图象与函数
的图象与函数 的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .
的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:填空题
已知P1(1,y1),P2(2,y2)是正比例函数 的图象上的两点,则y1 y2(填“>”或“<”或“=”).
的图象上的两点,则y1 y2(填“>”或“<”或“=”).
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西百色卷)数学(解析版) 题型:解答题
学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况,所得数据用表格与条形图描述如下:
科目 | 语文 | 数学 | 英语 | 体育 | 音乐 |
人数 | 10 | a | 15 | 3 | 2 |
(1)表格中a的值为 ;
(2)补全条形图;
(3)小李是最喜欢体育之一,小张是最喜欢音乐之一,计划从最喜欢体育、音乐的人中,每科目各选1人参加学校训练,用列表或树形图表示所有结果,并求小李、小张至少有1人被选上的概率是多少?

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西河池卷)数学(解析版) 题型:选择题
在 ABCD中,AC,BD是对角线,如果添加一个条件,即可推出
ABCD中,AC,BD是对角线,如果添加一个条件,即可推出 ABCD是矩形,那么这个条件是( )
ABCD是矩形,那么这个条件是( )
A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com