
【题目】如图,以O为圆心的弧![]() 度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
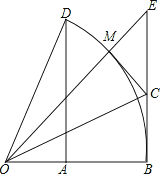
(1)求![]() 的值;
的值;
(2)若OE与![]() 交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
(3)在(2)的条件下,若BC=1,求tan∠BCO的值.
【答案】(1)![]() ;(2)理由见解析;(3)
;(2)理由见解析;(3)![]() +1.
+1.
【解析】
试题分析:(1)求出OB=BE,在Rt△OAD中,sin∠AOD=![]() ,代入求出即可;
,代入求出即可;
(2)求出∠BOC=∠MOC,证△BOC≌△MOC,推出∠CMO=∠OBC=90°,根据切线的判定推出即可;
(3)求出CM=ME,MC=BC,求出BC=MC=ME=1,在Rt△MCE中,根据勾股定理求出CE=![]() ,求出OB=
,求出OB=![]() +1,解直角三角形得出tan∠BCO=
+1,解直角三角形得出tan∠BCO=![]() +1,即可得出答案.
+1,即可得出答案.
试题解析:(1)∵EB⊥OB,∠BOE=45°,
∴∠E=45°,
∴∠E=∠BOE,
∴OB=BE,
在Rt△OAD中,sin∠AOD=![]() ,
,
∵OD=OB=BE,
∴![]() ;
;
(2)∵OC平分∠BOE,
∴∠BOC=∠MOC,
在△BOC和△MOC中,
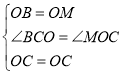
∴△BOC≌△MOC(SAS),
∴∠CMO=∠OBC=90°,
又∵CM过半径OM的外端,
∴CM为⊙O的切线;
(3)由(1)(2)证明知∠E=45°,OB=BE,△BOC≌△MOC,CM⊥ME,
∵CM⊥OE,∠E=45°,
∴∠MCE=∠E=45°,
∴CM=ME,
又∵△BOC≌△MOC,
∴MC=BC,
∴BC=MC=ME=1,
∵MC=ME=1,
∴在Rt△MCE中,根据勾股定理,得CE=![]() ,
,
∴OB=BE=![]() +1,
+1,
∵tan∠BCO=![]() ,OB=
,OB=![]() +1,BC=1,
+1,BC=1,
∴tan∠BCO=![]() +1.
+1.


科目:初中数学 来源: 题型:
【题目】⊙O的半径为7cm,点P到圆心O的距离OP=10cm,则点P与⊙O的位置关系为( )
A. 点P在圆上 B. 点P在圆内 C. 点P在圆外 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对点P(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x﹣y),且规定Pn(Pn+1(x,y))(n为大于1的整数).如P1(1,2)=(3,﹣1),P2(1,2)=P1(P1(1,2))=P1(3,﹣1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,﹣2),则P2016(0,﹣2)=( )
A. (0,21008) B. (0,﹣21008) C. (0,21009) D. (0,﹣21009)
查看答案和解析>>
科目:初中数学 来源: 题型:
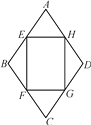
【题目】如图,四边形ABCD是一个菱形绿地,其周长为40![]() m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)
m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:如果存在实数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ,那么称这个函数是有上界函数,在所有满足条件的
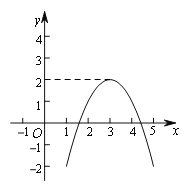
,那么称这个函数是有上界函数,在所有满足条件的![]() 中,其最小值称为这个函数的上确界.例如下图中的函数是有上界函数,其上确界是2.
中,其最小值称为这个函数的上确界.例如下图中的函数是有上界函数,其上确界是2.
(1)分别判断函数![]() (
(![]() )和
)和![]() (
(![]() )是不是有上界函数?如果是有上界函数,求其上确界;
)是不是有上界函数?如果是有上界函数,求其上确界;
(2)如果函数![]() (
(![]() )的上确界是
)的上确界是![]() ,且这个函数的最小值不超过
,且这个函数的最小值不超过![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若函数![]() (
(![]() )是以3为上确界的有上界函数,求
)是以3为上确界的有上界函数,求![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com