
【题目】对某一个函数给出如下定义:如果存在实数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ,那么称这个函数是有上界函数,在所有满足条件的
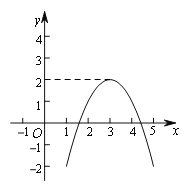
,那么称这个函数是有上界函数,在所有满足条件的![]() 中,其最小值称为这个函数的上确界.例如下图中的函数是有上界函数,其上确界是2.
中,其最小值称为这个函数的上确界.例如下图中的函数是有上界函数,其上确界是2.
(1)分别判断函数![]() (
(![]() )和
)和![]() (
(![]() )是不是有上界函数?如果是有上界函数,求其上确界;
)是不是有上界函数?如果是有上界函数,求其上确界;
(2)如果函数![]() (
(![]() )的上确界是
)的上确界是![]() ,且这个函数的最小值不超过
,且这个函数的最小值不超过![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若函数![]() (
(![]() )是以3为上确界的有上界函数,求
)是以3为上确界的有上界函数,求![]() 值.
值.
【答案】(1)y=![]() (x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;(2)-1≤a<1;(3)
(x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;(2)-1≤a<1;(3)![]() .
.
【解析】
试题分析:(1)根据有界函数函数的定义和上确界定义分析即可;
(2)根据函数的上确界和函数增减性得到2-a=b,函数的最小值为2-b,根据b>a,函数的最小值不超过2a+1,列不等式求解集即可;
(3)根据对称轴方程x=a和上确界为3,分类讨论a≤3时和a>3时,列方程求解.
试题解析:(1)根据有界函数定义,y=![]() (x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;
(x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;
(2)∵在y=-x+2中,y随x的增大而减小,
∴上确界为2-a,即2-a=b,
又b>a,所以2-a>a,解得a<1,
∵函数的最小值是2-b,∴2-b≤2a+1,得a≤2a+1,解得a≥-1,
综上所述:-1≤a<1;
(3)函数的对称轴为x=a,
①当a≤3时,函数的上确界是25-10a+2=27-10a,
∴27-10a=3,解得a=![]() ,符合题意;
,符合题意;
②当a>3时,函数的上确界是1-2a+2=3-2a,
∴3-2a=3,解得a=0,不符合题意.
综上所述:a=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,以O为圆心的弧![]() 度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
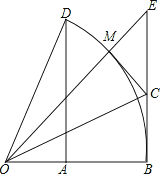
(1)求![]() 的值;
的值;
(2)若OE与![]() 交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
(3)在(2)的条件下,若BC=1,求tan∠BCO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列各式中,应填入﹣a的是( )
A.a12=﹣a13( )4
B.a12=(﹣a)5( )7
C.a12=﹣a4( )8
D.a12=a13+( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c为△ABC的三边长,关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0有两个相等的实数根,则△ABC为( )
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
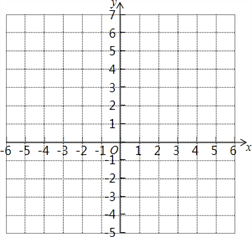
【题目】在如图所示的平面直角坐标系中表示下面各点:
A(2,0);B(1,-3);C(3,-5); D(-3,-5);E(3,5);F(5,7).
(1)A点到原点O的距离是 ______ .
(2)将点C向x轴的负方向平移6个单位,它与点 ______ 重合.
(3)连接CE,则直线CE与x轴,y轴分别是什么关系?
(4)点F到x、y轴的距离分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
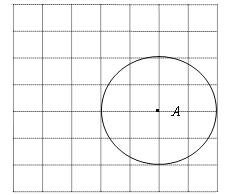
(1)根据A点坐标建立平面直角坐标系;
(2)将⊙A向左平移____________个单位长度与y轴首次相切,得到⊙A,并画出⊙A.此时点A的坐标为_____________.
(3)求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com