
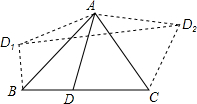
 如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2$\sqrt{3}$+2,D是BC边上异于B、C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是9+4$\sqrt{3}$.
如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2$\sqrt{3}$+2,D是BC边上异于B、C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是9+4$\sqrt{3}$. 分析 如图所示:过点D2作D2E⊥BC,垂足为E.设DC=x,则BD=2$\sqrt{3}+2$-x.然后根据四边形D1BCD2的面积等于梯形D1BED2的面积减去三角形CED2的面积列函数关系是求解即可.
解答 解:如图所示:过点D2作D2E⊥BC,垂足为E.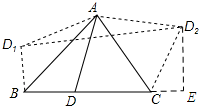
设DC=x,则BD=2$\sqrt{3}+2$-x.
由翻折的性质可知:∠D1BD=90°,∠ECD2=60°,D1B=BD=2$\sqrt{3}+2$-x,CD2=DC=x.
∵在Rt△CED2中,∠ECD2=60°
∴EC=$\frac{1}{2}x$,D2E=$\frac{\sqrt{3}}{2}x$.
∴${S}_{{D}_{1}BC{D}_{2}}$=${S}_{{D}_{1}BE{D}_{2}}$-${S}_{△CE{D}_{2}}$
=$\frac{1}{2}$(D1B+D2E)•BE-$\frac{1}{2}×CE×E{D}_{2}$
=$\frac{1}{2}×$(2$\sqrt{3}$+2-x+$\frac{\sqrt{3}}{2}x$)(2$\sqrt{3}$+2+$\frac{1}{2}x$)-$\frac{1}{2}×\frac{1}{2}x×\frac{\sqrt{3}}{2}x$
=$-\frac{1}{4}$(x-2)2+9+4$\sqrt{3}$.
∴当x=2时,四边形D1BCD2的面积有最大值,最大值为9+4$\sqrt{3}$.
故答案为:9+4$\sqrt{3}$.
点评 本题主要考查的是翻折的性质、二次函数的综合应用,根据题意列出函数关系式是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:填空题
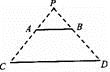
如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,横杆AB与CD的距离是3m,则P到AB的距离是 m.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:解答题
图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
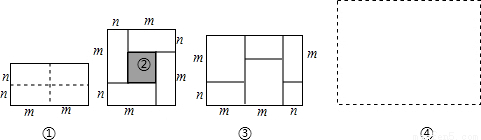
(1)请用两种不同的方法求图②中阴影部分的面积.
方法1:
方法2:
请你写出下列三个代数式: 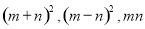 之间的等量关系.
之间的等量关系.
;
(2)根据(1)题中的等量关系,解决如下问题:
已知: 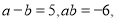 则
则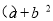 =
=
(3)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示的代数恒等式是___ .
(4)已知等式: 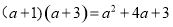 ,请你在图④中画出一个相应的几何图形。
,请你在图④中画出一个相应的几何图形。
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
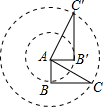 如图,Rt△ABC中,AC=$\sqrt{5}$,以点A为中心逆时针旋转90°得到Rt△AB′C′,则Rt△A′B′C′,则$\widehat{CC′}$的长为$\frac{\sqrt{5}}{2}$π.
如图,Rt△ABC中,AC=$\sqrt{5}$,以点A为中心逆时针旋转90°得到Rt△AB′C′,则Rt△A′B′C′,则$\widehat{CC′}$的长为$\frac{\sqrt{5}}{2}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25(1+a%)2=18 | B. | 25(1-a%)2=18 | C. | 25(1-2a%)=18 | D. | 25(1-a2%)=18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com