

���� ��1������ת�����ʵó����ۣ������жϳ���AOB�ա�COD�ó�CO=OA=3��OD=OB=4�����ɵó���C��D���꣬�ô���ϵ�������ɵó����ۣ�
��2�����ɣ�1�����ۺ�ͬ�ǵ��������жϳ�����BOE�ա�DOF�����ɵó���EOF�ǵ���ֱ�������Σ����ɵó����ۣ�
����ȷ������E�����꣬�ٽ����ٵĽ����жϳ���OHE�ա�OGF�����ɵó�OG=OH��FG=EH���ɵó�F�����ꣻ
��3���������������ȫ�������ε����ʺ�������Ǻ�������ȷ������P�����꣮
��� �⣺��1����ֱ��y=-$\frac{4}{3}$x+4��x�ᣬy��ֱ��ڵ�A����B��
��A��3��0����B��0��4����
��OA=3��OB=4��
�ߡ�AOB������ԭ����ʱ����ת90��õ���COD��
���AOB�ա�COD��
��CO=OA=3��OD=OB=4��
��C��0��3����D��-4��0����
��ֱ��CD �Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{b=3}\\{-4k+b=0}\end{array}\right.$��
��$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$��
��ֱ��CD �Ľ���ʽΪy=$\frac{3}{4}$x+3��
��2�����ɣ�1��֪����AOB�ա�COD��
��OB=OD����ABO=��CDO��
��OF��OE����COF+��COE=90�㣬
�ߡ�COE+��DOF=90�㣬
���BOE=��DOF��
�ڡ�BOE�͡�DOF�У�$\left\{\begin{array}{l}{��BOE=��DOF}\\{OB=OD}\\{��ABO=��CDO}\end{array}\right.$��
���BOE�ա�DOF��
��OE=OF��
�ߡ�EOF=90�㣬
���EOF�ǵ���ֱ�������Σ�
���OEF=45�㣻
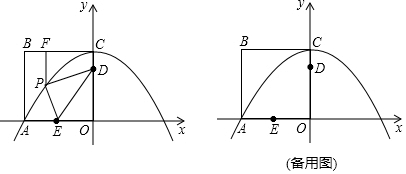
�ڣ���ͼ2�� ��ֱ��AB�Ľ���ʽΪy=-$\frac{4}{3}$x+4�٣�
��ֱ��AB�Ľ���ʽΪy=-$\frac{4}{3}$x+4�٣�
�ɣ�1��֪��ֱ��CD �Ľ���ʽΪy=$\frac{3}{4}$x+3�ڣ�
�����٢ڵã�E��$\frac{12}{25}$��$\frac{84}{25}$����
����F��FG��OD������E��EH��OB��
�ɢ�֪����BOE�ա�DOF��
���BOE=��DOF��OE=OF
�ڡ�OHE�͡�OGF�У�$\left\{\begin{array}{l}{��OHE=��OGF=90��}\\{��BOE=��DOF}\\{OE=OF}\end{array}\right.$��
���OHE�ա�OGF��
��OG=OH=$\frac{84}{25}$��FG=EH=$\frac{12}{25}$
��F��-$\frac{84}{25}$��$\frac{12}{25}$����
��3����ͼ1��
�١�DP'Q'=90�㣬
�ߡ�P'Q'D�ա�OCD��
��DP'=OD=4��
�ߡ�CDO=��P'DQ'��
��cos��P'DQ'=$\frac{4}{5}$��sin��P'DQ'=$\frac{3}{5}$��
��P'H��x�ᣬ��DH=DP'•cos��PDQ=$\frac{16}{5}$��P'H=DP'•cos��PDQ=$\frac{12}{5}$��
��OH=OD+DH=$\frac{36}{5}$
���P'���꣨-$\frac{36}{5}$��-$\frac{12}{5}$����
�ڡ�DQP=90�㣬
�ߡ�PQD�ա�COD����SAS��
��DQ=OD=4��PQ=3��
���P���꣨-8��-3����
�ۡ�DP''Q''=90�㣬
�ߡ�P''Q''D�ա�OCD����SAS��
��DP''=OD=4��P''Q''=OC=3��
��P''G=DP''•sin��CDO=$\frac{12}{5}$��DG=DP''•cos��CDO=$\frac{16}{5}$��
��OG=$\frac{4}{5}$��
���P���꣨-$\frac{4}{5}$��$\frac{12}{5}$����
������DPQ�͡�DOCȫ��ʱ����P������Ϊ��-$\frac{36}{5}$��-$\frac{12}{5}$������-8��-3������-$\frac{4}{5}$��$\frac{12}{5}$����
���� ������һ�κ����ۺ��⣬��Ҫ�����˴���ϵ������ȫ�������ε��ж������ʣ�����ֱ�������ε��ж������ʣ��жϳ���BOE�ա�DOF�ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
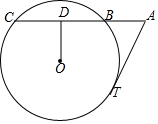 ��ͼ��AT�ǡ�O�����ߣ�OD��BC�ڵ�D������AT=10cm��AC=20cm��OD=4cm����뾶OC=��������
��ͼ��AT�ǡ�O�����ߣ�OD��BC�ڵ�D������AT=10cm��AC=20cm��OD=4cm����뾶OC=��������| A�� | 8.5cm | B�� | 8cm | C�� | 9.5cm | D�� | 9cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a}{m}$+$\frac{b}{m}$=$\frac{a+b}{2m}$ | B�� | $\frac{a}{x-y}$-$\frac{a}{y-x}$=0 | C�� | 1+$\frac{1}{a}$=$\frac{2}{a}$ | D�� | $\frac{x}{x+y}$+$\frac{y}{x+y}$=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
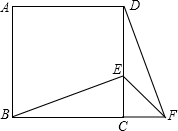 ��ͼ����������ABCD�У�EλDC���ϵĵ㣬����BE������BCE�Ƶ�C˳ʱ�뷽����ת90��õ���DCF������EF������BEC=60�㣬���EFD�Ķ���Ϊ��������
��ͼ����������ABCD�У�EλDC���ϵĵ㣬����BE������BCE�Ƶ�C˳ʱ�뷽����ת90��õ���DCF������EF������BEC=60�㣬���EFD�Ķ���Ϊ��������| A�� | 15�� | B�� | 10�� | C�� | 20�� | D�� | 25�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 11��13 | B�� | 13��15 | C�� | 11 | D�� | 13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��-1 | B�� | m��1 | C�� | m��1 | D�� | m��-1��m��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У���BAC=90�㣬ADΪBC�������ߣ���AD=$\sqrt{5}$����ABC�ܳ�Ϊ6+2$\sqrt{5}$�����ABC�����Ϊ4��
��ͼ����ABC�У���BAC=90�㣬ADΪBC�������ߣ���AD=$\sqrt{5}$����ABC�ܳ�Ϊ6+2$\sqrt{5}$�����ABC�����Ϊ4���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com