
如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求 的长.
的长.

图1 图2
(1)BE=FH ;理由见解析
(2)证明见解析
(3) =2π
=2π
【解析】
试题分析:(1)由△ABE≌△EHF(SAS)即可得到BE=FH
(2)由(1)可知AB=EH,而BC=AB,FH=EB,从而可知△FHC是等腰直角三角形,∠FCH为45°,而∠ACB也为45°,从而可证明
(3)由已知可知∠EAC=30°,AF是直径,设圆心为O,连接EO,过点E作EN⊥AC于点N,则可得△ECN为等腰直角三角形,从而可得EN的长,进而可得AE的长,得到半径,得到 所对圆心角的度数,从而求得弧长
所对圆心角的度数,从而求得弧长
试题解析:(1)BE=FH。理由如下:
∵四边形ABCD是正方形 ∴∠B=90°,
∵FH⊥BC ∴∠FHE=90°
又∵∠AEF=90° ∴∠AEB+∠HEF=90° 且∠BAE+∠AEB=90°
∴∠HEF=∠BAE ∴ ∠AEB=∠EFH 又∵AE=EF
∴△ABE≌△EHF(SAS)
∴BE=FH
(2)∵△ABE≌△EHF
∴BC=EH,BE=FH 又∵BE+EC=EC+CH ∴BE=CH
∴CH=FH
∴∠FCH=45°,∴∠FCM=45°
∵AC是正方形对角线,∴ ∠ACD=45°
∴∠ACF=∠FCM +∠ACD =90°
(3)∵AE=EF,∴△AEF是等腰直角三角形
△AEF外接圆的圆心在斜边AF的中点上。设该中点为O。连结EO得∠AOE=90°

过E作EN⊥AC于点N
Rt△ENC中,EC=4,∠ECA=45°,∴EN=NC=
Rt△ENA中,EN =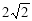
又∵∠EAF=45° ∠CAF=∠CEF=15°(等弧对等角)
∴∠EAC=30°
∴AE=
Rt△AFE中,AE= = EF,∴AF=8
= EF,∴AF=8
AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°
 =2π·4·(90°÷360°)=2π
=2π·4·(90°÷360°)=2π
考点:1、正方形;2、等腰直角三角形;3、圆周角定理;4、三角函数


科目:初中数学 来源:2014年初中毕业升学考试(广西河池卷)数学(解析版) 题型:填空题
如图,小明从A地沿北偏东60°方向走2千米到B地,再从B地向正南方向走3千米到C地,此时小明距离A地 千米(结果可保留根号).

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西桂林卷)数学(解析版) 题型:选择题
如图,已知AB∥CD,∠1=56°,则∠2的度数是( )

A.34° B.56° C.65° D.124°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西崇左卷)数学(解析版) 题型:选择题
如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
作法:
①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E;
②分别以D,E为圆心,大于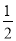 DE的长为半径画弧,两弧在∠AOB内交于一点C;
DE的长为半径画弧,两弧在∠AOB内交于一点C;
③画射线OC,射线OC就是∠AOB的角平分线.

A.ASA B.SAS C.SSS D.AAS
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西崇左卷)数学(解析版) 题型:选择题
在2014年5月崇左市教育局举行的“经典诗朗诵”演讲比赛中,有11名学生参加决赛,他们决赛的成绩各不相同,其中的一名学生想知道自己能否进入前6名,不仅要了解自己的成绩,还要了解这11名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西北海卷)数学(解析版) 题型:解答题
已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使得⊙O经过A、C两点,且圆心O落在AB边上.(要求尺规作图,保留作图痕迹,不必写作法)
(2)求证:BC是(1)中所作⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com