
分析 (1)用P(a,b)表示△OAB内的格点,a,b为正整数,假设结论不成立,则点P位于某条线段OCi内部.如图,过点P作PE⊥OB于点E,过点Ci作CiF⊥AB于点F.
由△OEP∽△OFCi,知$\frac{b}{a}$=$\frac{p-i}{i}$,得到i≤a,这与a<i矛盾.得到原结论成立.
(2)假设结论不成立,即p为质数,故p=xy,其中x,y∈N,且2≤x,y≤p-1,因为△OAB内部的格点的横、纵坐标之和可以是从2到p-1之间的任何整数,故必存在一格点P(a,b)满足a+b=x,得到点P(a,b)在线段OCi内部,即在线段OC上除端点外还有其它格点,这与已知矛盾.得到原结论成立.
解答 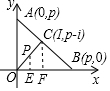 解:(1)用P(a,b)表示△OAB内的格点,a,b为正整数,
解:(1)用P(a,b)表示△OAB内的格点,a,b为正整数,
假设结论不成立,则点P位于某条线段OCi内部.
如图,过点P作PE⊥OB于点E,过点Ci作CiF⊥AB于点F.
由△OEP∽△OFCi,知$\frac{b}{a}$=$\frac{p-i}{i}$,
其中1≤i≤p-1,
则1≤a≤i,1≤b≤p-i,
由$\frac{b}{a}$=$\frac{p-i}{i}$,知(a+b)i=ap,
则i|ap,
因为p为质数,且1≤i≤p-1,
则i与p互质,
则i|a,
故i≤a,
这与a<i矛盾.
所以,假设不成立,
所以原结论成立.
(2)假设结论不成立,即p为质数,故p=xy,其中x,y∈N,且2≤x,y≤p-1,
因为△OAB内部的格点的横、纵坐标之和可以是从2到p-1之间的任何整数,
故必存在一格点P(a,b)满足a+b=x,
则(a+b)y=xy=p,即ay+by=p,
故点(ay,by)必是C1(1,p-1),…,Ci(i,p-i),…,Cp-1(p-1,1)中的一个点,
设为Ci(i,p-i),
则有ya=i,by=p-i,
故$\frac{b}{a}$=$\frac{p-i}{i}$,
所以点P(a,b)在线段OCi内部,即在线段OC上除端点外还有其它格点,这与已知矛盾.
故原结论成立.
点评 此题考查了质数与合数,是竞赛题型,难度较大,本题关键是通过假设法,得到矛盾的结论,从而求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
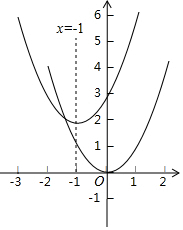 在学完《二次函数》后,老师给小明布置了家庭作业:完成下列表格,再用描点法在同一坐标系中画出y1与y2的函数图象.
在学完《二次函数》后,老师给小明布置了家庭作业:完成下列表格,再用描点法在同一坐标系中画出y1与y2的函数图象.| x | … | 0 | 1 | 2 |
| y1=ax2 | … | 0 | 1 | 4 |
| y2=ax2+bx+c | … | 3 | 6 | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com