
【题目】如图:公路旁有两个高度相等的路灯AB、CD.小明同学上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
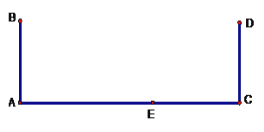
(1)在图中画出小明的位置,并画出光线,标明(太阳光、灯光).
(2)若AC距离为80米,小明身高为1.5米,小明离里程碑E恰好5米,求路灯高.
【答案】(1)画图见解析,详情见解析;(2)6米;
【解析】
(1)由图,GH所在位置就是小明的位置,所以DG为灯光,连接太阳光线BE,过点C作BE的平行线CG,即图中BE、CG是太阳光,DG为灯光;
(2)由GH⊥AC,CD⊥AC,可得GH∥CD,从而得△EGH∽△EDC,即![]() ;又CG∥BE,可得∠GCE=∠BEA,因为GH⊥AC,AB⊥AC,所以∠BAC=∠GHC=90°,推出∠GCE=∠BEA,∠BAC=∠GHC,得到△GCH∽△BEA,即
;又CG∥BE,可得∠GCE=∠BEA,因为GH⊥AC,AB⊥AC,所以∠BAC=∠GHC=90°,推出∠GCE=∠BEA,∠BAC=∠GHC,得到△GCH∽△BEA,即![]() ;再根据题意可得GH=1.5米,EH=5米,AC=80米,AB=CD,可设AB=x米,因为
;再根据题意可得GH=1.5米,EH=5米,AC=80米,AB=CD,可设AB=x米,因为![]() ,
,![]() ,AB=CD,可得
,AB=CD,可得![]() ,即
,即![]() ,把数值代入
,把数值代入![]() 和
和![]() 得,
得,
解得x=6,即AB=CD=6米;
解:
(1)如图,GH所在位置就是小明的位置,连结BE、DE,过C作CG∥BE与DE相交于点G,过G作GH⊥AC,即图中BE、CG是太阳光,DG为灯光;
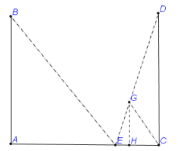
(2)如图,GH所在位置就是小明的位置,

连结BE、DE,过C作CG∥BE与DE相交于点G,过G作GH⊥AC,即图中BE、CG是太阳光,DG为灯光;
∵GH⊥AC,CD⊥AC,
∴GH∥CD,
∴△EGH∽△EDC,
∴![]() ,
,
∵CG∥BE,
∴∠GCE=∠BEA,
∵GH⊥AC,AB⊥AC,
∴∠BAC=∠GHC=90°,
∵∠GCE=∠BEA,∠BAC=∠GHC,
∴△GCH∽△BEA,
∴![]() ,
,
根据题意可得GH=1.5米,EH=5米,AC=80米,AB=CD,可设AB=x米,
∵![]() ,
,![]() ,AB=CD,
,AB=CD,
∴![]() ,
,
∴![]() ,
,
将GH=1.5米,EH=5米,AC=80米,AB=CD,AB=x米代入![]() 和
和![]() 得,
得,
![]() ,
,![]() ,
,
联立两式,解得x=6,
即AB=CD=6米,
路灯的高为6米;


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
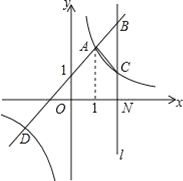
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=![]() x2-2x,直线y2=-2x+b相交于A,B两点,其中点A的横坐标为2.当x任取一值时,x对应的函数值分别为y1,y2,取m=
x2-2x,直线y2=-2x+b相交于A,B两点,其中点A的横坐标为2.当x任取一值时,x对应的函数值分别为y1,y2,取m=![]() (|y1-y2|+y1+y2).则
(|y1-y2|+y1+y2).则

A. 当x<-2时,m=y2.B. m随x的增大而减小.
C. 当m=2时,x=0.D. m≥-2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中留个形状大小都相同的四边形围成一个圆的内接六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为![]() cm2,则该圆的半径为________cm.
cm2,则该圆的半径为________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月17日,我国第一艘国产航母“山东舰”在海南三亚交付海军.如图,“山东舰”在一次试水测试中,航行至![]() 处,观测指挥塔
处,观测指挥塔![]() 位于南偏西
位于南偏西![]() 方向,在沿正南方向以30海里/小时的速度匀速航行2小时后,到达
方向,在沿正南方向以30海里/小时的速度匀速航行2小时后,到达![]() 处,再观测指挥塔
处,再观测指挥塔![]() 位于南偏西
位于南偏西![]() 方向,若继续向南航行.求“山东舰”与指挥塔之间的最近距离为多少海里?(结果保留根号)
方向,若继续向南航行.求“山东舰”与指挥塔之间的最近距离为多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com