
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 、
、![]() 在
在![]() 上,且
上,且![]() ,四边形
,四边形![]() 的面积为__________.
的面积为__________.
【答案】4
【解析】
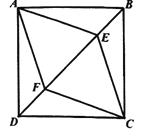
连结AC,交BD于点O,依据正方形的性质可得到AC⊥EF,然后再证明OE=OF,从而可得到四边形AFCE为平行四边形,于是可证明它是一个菱形;先求得BF的长,然后可得到OF的长,进而可得到EF的长,依据依据菱形的面积等于两对角线乘积的一半求解即可.
解:连结AC,交BD于点O.

∵四边形ABCD是正方形,
∴OA=OC,OB=OD.
又∵BE=DF,
∴BO - BE =DO-DF即OE=OF.
∴四边形AFCE是平行四边形.
∵BD⊥AC,
∴四边形AFCE是菱形.
∵AB=AD=2![]() ,
,
∴由勾股定理可知AC=BD=4,
∵DF=BE=1,
∴EF=2,
∴菱形的面积=![]() EFAC=
EFAC=![]() ×2×4=4,
×2×4=4,
故答案为:4.


科目:初中数学 来源: 题型:
【题目】已知,点![]() 和点
和点![]() 是线段
是线段![]() 的两个端点,线段
的两个端点,线段![]() ,点
,点![]() 是点
是点![]() 和点
和点![]() 的对称中心,点
的对称中心,点![]() 是点
是点![]() 和点
和点![]() 的对称中心,以此类推,(图中未画出)点
的对称中心,以此类推,(图中未画出)点![]() 是点
是点![]() 和点
和点![]() 的对称中心.(
的对称中心.(![]() 为正整数)
为正整数)
![]()
(1)填空:线段![]() ____________ ;线段
____________ ;线段![]() _____________ (用含
_____________ (用含![]() 的最简代数式表示)
的最简代数式表示)
(2)试写出线段![]() 的长度(用含
的长度(用含![]() 和
和![]() 的代数式表示,无需说明理由)
的代数式表示,无需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
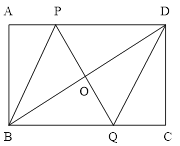
【题目】如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.
(1) 求证:四边形PBQD是平行四边形
(2) 若AD=6cm,AB=4cm, 点P从点A出发,以1cm/s的速度向点D运动(不与点D重合),设点P运动时间为t s , 请用含t的代数式表示PD的长,并求出当t为何值时,四边形PBQD是菱形。并求出此时菱形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
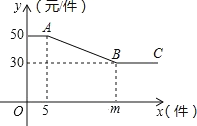
【题目】某商店经销某种玩具,该玩具每个进价 20 元,为进行促销,商店制定如下“优惠” 方案:如果一次销售数量不超过 5 个,则每个按 50 元销售:如果一次销售数量超过 5 个,则每增加一个,所有玩具均降低 1 元销售,但单价不得低于 30 元,一次销售该玩具的单价 y(元)与销售数量 x(个)之间的函数关系如下图所示.
(1)结合图形,求出 m 的值;射线 BC 所表示的实际意义是什么;
(2)求线段 AB 满足的 y 与 x 之间的函数解析式,并直接写出自变量的取值范围;
(3)当销售 15 个时,商店的利润是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,且OA=OB
(1)求证:四边形ABCD是矩形;
(2)若AB=5,∠AOB=60°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
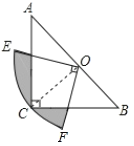
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从相距100km的A、B两地同时出发相向而行,并以各自的速度匀速行驶.甲出发2h后到达B地立即按原路返回,返回时速度提高了30km/h,回到A地后在A地休息等乙,乙在出发5h后到达A地.(友情提醒:可以借助用线段图分析题目)
(1)乙的速度是_______![]() ,甲从A地到B地的速度是_______
,甲从A地到B地的速度是_______![]() ,甲在出发_______小时到达A地.
,甲在出发_______小时到达A地.
(2)出发多长时间两人首次相遇?
(3)出发多长时间时,两人相距30千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有个点A(﹣1,0),点A第1次向上跳动1个单位至点A1(﹣1,1),紧接着第2次向右跳动2个单位至点A2(1,1),第3次向上跳动1个单位至点A3,第4次向左跳动3个单位至点A4,第5次又向上跳动1个单位至点A5,第6次向右跳动4个单位至点A6,……,依此规律跳动下去,点A第2019次跳动至点A2019的坐标是____.
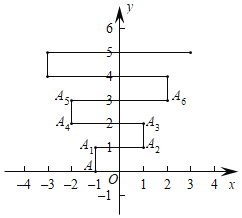
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点E在边AB上,连接DE,取DE的中点F,连接EO并延长交CD于点G.若BE=3CG,OF=2,则线段AE的长是_____.
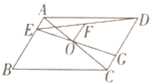
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com