
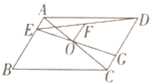
【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点E在边AB上,连接DE,取DE的中点F,连接EO并延长交CD于点G.若BE=3CG,OF=2,则线段AE的长是_____.
【答案】![]() .
.
【解析】
已知点O是对角线AC的中点,DE的中点为F,可得OF为△EDG的中位线,根据三角形的中位线定理可得DG=2OF=4;由平行四边形的性质可得AB∥CD,AB=CD,即可得∠EAO=∠GCO,再判定△AOE≌△COG,根据全等三角形的性质可得AE=CG,即可得BE=DG=4,再由BE=3CG即可求得AE=CG=![]() .
.
∵点O是对角线AC的中点,DE的中点为F,
∴OF为△EDG的中位线,
∴DG=2OF=4;
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠EAO=∠GCO,
在△AOE和△COG中,
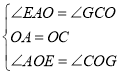 ,
,
∴△AOE≌△COG,
∴AE=CG,
∵AB=CD,
∴BE=DG=4,
∵BE=3CG,
∴AE=CG=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
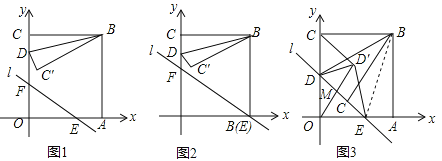
【题目】(2016浙江省衢州市)如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.
(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且![]() 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
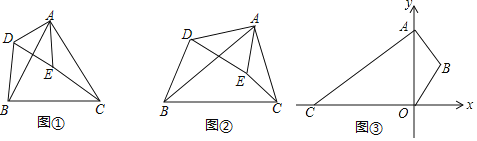
(探究)如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
(应用)如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,把表示数![]() 的点称为基准点,记作点
的点称为基准点,记作点![]() .对于两个不同的点
.对于两个不同的点![]() 和
和![]() ,若点
,若点![]() 、点
、点![]() 到点
到点![]() 的距离相等,则称点
的距离相等,则称点![]() 和点
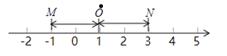
和点![]() 互为基准变换点.例如:下图中,点
互为基准变换点.例如:下图中,点![]() 表示数
表示数![]() ,点N表示数
,点N表示数![]() ,它们与基准点
,它们与基准点![]() 的距离都是
的距离都是![]() 个单位长度,点
个单位长度,点![]() 与点
与点![]() 互为基准变换点.
互为基准变换点.
(1)已知点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 与点
与点![]() 互为基准变换点.
互为基准变换点.
①若![]() ,则
,则![]() _______ ;
_______ ;
②用含![]() 的式子表示
的式子表示![]() ,则
,则![]() _____;
_____;
(2)对点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以
表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动
,再把所得数表示的点沿着数轴向左移动![]() 个单位长度得到点
个单位长度得到点![]() .若点
.若点![]() 与点
与点![]() 互为基准变换点,则点
互为基准变换点,则点![]() 表示的数是_____________;
表示的数是_____________;
(3)点![]() 在点
在点![]() 的左边,点
的左边,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度.对
个单位长度.对![]() 、
、![]() 两点做如下操作:点
两点做如下操作:点![]() 沿数轴向右移动
沿数轴向右移动![]() 个单位长度得到
个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动
沿数轴向右移动![]() 个单位长度得到
个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .
.![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
,![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .若无论
.若无论![]() 为何值,
为何值,![]() 与
与![]() 两点间的距离都是
两点间的距离都是![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买A、B两种型号电脑。已知每台A种型号电脑价格比每台B种型号电脑价格多0.1万元,且用10万元购买A种型号电脑的数量与用8万元购买B种型号电脑的数量相同.
(1)求A、B两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,则最多可购买A种型号电脑多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
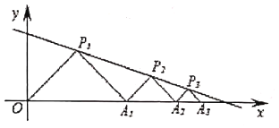
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,…都是等腰直角三角形,其直角顶点
,…都是等腰直角三角形,其直角顶点![]() ,
,![]() ,
,![]() ,…均在直线
,…均在直线![]() 上.设
上.设![]() ,
,![]() ,
,![]() ,…的面积分别为
,…的面积分别为![]() ,
,![]() ,
,![]() ,…,根据图形所反映的规律,
,…,根据图形所反映的规律,![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
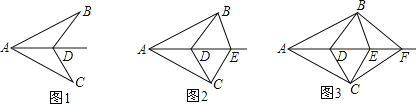
【题目】已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、BE、CE、BF、CF,图中有6对全等三角形;依此规律,第n个图形中有_____对全等三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com