
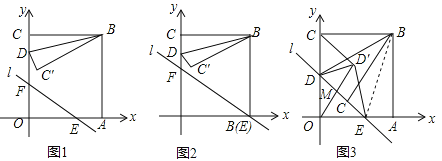
����Ŀ����2016�㽭ʡ�����У���ͼ1����ֱ������ϵxoy�У�ֱ��l��y=kx+b��x�ᣬy���ڵ�E��F����B�������ǣ�2��2��������B�ֱ���x�ᡢy��Ĵ��ߣ�����ΪA��C����D���߶�CO�ϵĶ��㣬��BDΪ�Գ��ᣬ������BCD����ԳƵ���BC��D��
��1������CBD=15��ʱ�����C�������꣮
��2����ͼ1�е�ֱ��l������A����![]() ʱ����ͼ2�������D��C��O���˶������У��߶�BC��ɨ����ͼ������OAF�ص����ֵ������
ʱ����ͼ2�������D��C��O���˶������У��߶�BC��ɨ����ͼ������OAF�ص����ֵ������
��3����ͼ1�е�ֱ��l������D��C��ʱ����ͼ3������DEΪ�Գ��ᣬ������DOE����ԳƵ���DO��E������O��C��O��O�����Ƿ���ڵ�D��ʹ����DO��E����CO��O���ƣ������ڣ����k��b��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��C�䣨![]() ��1������2��
��1������2��![]() ����3�����ڣ�k=
����3�����ڣ�k=![]() ��b=1��
��b=1��
�����������⣨1�����÷��۱任�����ʵó���CBD=��C��BD=15�㣬C��B=CB=2�������ó�CH�ij��������ó��𰸣�
��2���������ֱ��AF�Ľ���ʽ�������ó���D��O�غ�ʱ����C����A�غϣ���BC��ɨ����ͼ������OAF�غϲ����ǹ��Σ�������ɣ�
��3����������ó���DO��E����COO�����ƣ�����COO������Rt���������ó�Rt��BAE��Rt��BC��E��HL���������ù��ɶ������EO�ij������ó��𰸣�
�����������1���ߡ�CBD�ա�C��BD�����CBD=��C��BD=15�㣬C��B=CB=2�����CBC��=30������ͼ1����C��H��BC��H����C��H=1��HB=![]() ����CH=
����CH=![]() �����C������������
�����C������������![]() ��1����
��1����
��2����ͼ2����A��2��0����![]() �������ֱ��AF�Ľ���ʽΪ��
�������ֱ��AF�Ľ���ʽΪ��![]() ����b=
����b=![]() ����ֱ��AF�Ľ���ʽΪ��
����ֱ��AF�Ľ���ʽΪ��![]() �����OAF=30�㣬��BAF=60�㣬���ڵ�D��C��O���˶������У�BC��ɨ����ͼ�������Σ��൱D��O�غ�ʱ����C����A�غϣ���BC��ɨ����ͼ������OAF�غϲ����ǹ��Σ���C����ֱ��
�����OAF=30�㣬��BAF=60�㣬���ڵ�D��C��O���˶������У�BC��ɨ����ͼ�������Σ��൱D��O�غ�ʱ����C����A�غϣ���BC��ɨ����ͼ������OAF�غϲ����ǹ��Σ���C����ֱ��![]() ��ʱ��BC��=BC=AB�����ABC���ǵȱ������Σ���ʱ��ABC��=60�㣬���ص����ֵ�����ǣ�
��ʱ��BC��=BC=AB�����ABC���ǵȱ������Σ���ʱ��ABC��=60�㣬���ص����ֵ�����ǣ�![]() =
=![]() ��
��
��3����ͼ3����OO����DE���ڵ�M����O��M=OM��OO����DE������DO��E����COO�����ƣ�����COO������Rt�����ڵ�D��C��O���˶������У���COO������Ȼֻ�ܡ�CO��O=90�㣬��CO����DE����CD=OD=1����b=1������BE������Գ��Կ�֪C��D=CD��BC��=BC=BA����BC��E=��BCD=��BAE=90������Rt��BAE��Rt��BC��E������BE=BE��AB=BC�䣬��Rt��BAE��Rt��BC��E��HL������AE=C��E����DE=DC��+C��E=DC+AE����OE=x����AE=2��x����DE=DC+AE=3��x���ɹ��ɶ����ã�![]() ����ã�x=
����ã�x=![]() ����D��0��1����E��
����D��0��1����E��![]() ��0������
��0������![]() ����ã�k=
����ã�k=![]() ������ڵ�D��ʹ��DO��E����COO�����ƣ���ʱk=
������ڵ�D��ʹ��DO��E����COO�����ƣ���ʱk=![]() ��b=1��
��b=1��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
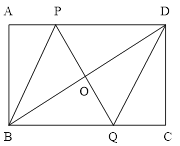
����Ŀ����ͼ���ھ���ABCD�У�P��AD��һ���㣬OΪBD���е㣬����PO���ӳ�����BC�ڵ�Q.
(1) ��֤���ı���PBQD��ƽ���ı���
(2) ��AD=6cm,AB=4cm, ��P�ӵ�A��������1cm/s���ٶ����D�˶��������D�غϣ������P�˶�ʱ��Ϊt s , ���ú�t�Ĵ���ʽ��ʾPD�ij����������tΪ��ֵʱ���ı���PBQD�����Ρ��������ʱ���ε��ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˷ֱ�����100km��A��B����ͬʱ�����������,���Ը��Ե��ٶ�������ʻ���׳���2h��B��������ԭ·���أ�����ʱ�ٶ������30km/h���ص�A�غ���A����Ϣ���ң����ڳ���5h��A�أ�(�������ѣ����Խ������߶�ͼ������Ŀ��
��1���ҵ��ٶ���_______![]() ���״�A�ص�B�ص��ٶ���_______
���״�A�ص�B�ص��ٶ���_______![]() �����ڳ���_______Сʱ����A�أ�
�����ڳ���_______Сʱ����A�أ�
��2�������ʱ�������״�������
��3�������ʱ��ʱ���������30ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
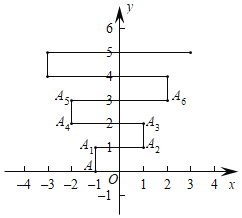
����Ŀ����ͼ����ƽ��ֱ������ϵ���и���A(��1��0)����A��1����������1����λ����A1(��1��1)�������ŵ�2����������2����λ����A2(1��1)����3����������1����λ����A3����4����������3����λ����A4����5������������1����λ����A5����6����������4����λ����A6�����������˹���������ȥ����A��2019����������A2019��������____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���A��x�Ḻ�����ϣ�����B��x���������ϣ���������p=ax2-10ax+8��a��0��������C��D�����B������Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��DΪBC�е㣬AE��BD����AE=BD.
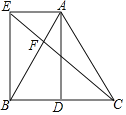
��1����֤���ı���AEBD�Ǿ��Σ�
��2������CE��AB�ڵ�F����BE=2![]() ��AE=2����EF�ij���
��AE=2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ����ش���������
��ͼ1����ABΪ�ᣬ�ѡ�ABC����180�㣬���Ա任����ABD��λ�ã�
��ͼ2���ѡ�ABC������ACƽ�ƣ����Ա任����DEF��λ�ã������������е�һ������������һ�������ξ����ۡ�ƽ�Ƶȷ����任�ɵģ�����ֻ�ı�λ�ã����ı���״��С��ͼ�α任���������ε�ȫ�ȱ任������ѧϰС����������ε�ȫ�ȱ任������̽��������
��1������д��һ��ȫ�ȱ任�ķ����������ۡ�ƽ���⣩���� ����
��2����ͼ2��ǰ��С��ѡ�ABC������ACƽ�Ƶ���DEF����ƽ�Ƶľ���Ϊ2����AC��5����DC���� ����
��3����ͼ3��Բ��С��չ����̽������ѡ�ABCֽƬ��DE�۵���ʹ��A�����ı���BCDE�ڲ���A���λ�ã��ҵó�һ�����ۣ�2��A�䣽��1+��2�������������۸���֤����
��4����ͼ4���ܽ�С�������������ѡ�ABCֽƬ��DE�۵���ʹ��A�����ı���BCDE�ⲿ��A���λ�ã���ʱ��A�����1����2֮����ۻ��������������������֤��������������д����ȷ���۲�֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У���O�ǶԽ���AC���е㣬��E�ڱ�AB�ϣ�����DE��ȡDE���е�F������EO���ӳ���CD�ڵ�G����BE=3CG��OF=2�����߶�AE�ij���_____��
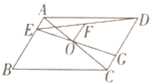
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳��һ����ѧ�κ���ʦ������һ���κ���ϰ�⣺
��ͼ����֪��Rt��ABC�У�AC=BC����ACB=90����CD��AB�ڵ�D����E��F�ֱ���A��BC�ϣ���1=��2��FG��AB�ڵ�G����֤����CDE�ա�EGF��
��1���Ķ����⣬��ɽ��
����֤����˼·�������п�ͼ��ʾ��
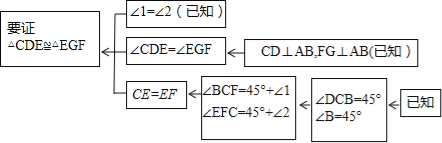
��������˼·��������������д�����ϰ���֤�����̣�
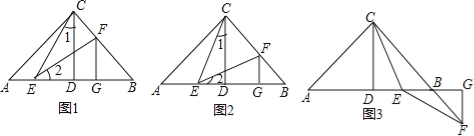
��2������λ�ã�֤������
��CEƽ����ACD�������������䣬��֤��AE=BF��
��3��֪ʶǨ�ƣ�̽������
��ͼ����֪��Rt��ABC�У�AC=BC����ACB=90����CD��AB�ڵ�D������E��DB���е㣬��F��ֱ��CB��������EC=EF����ֱ��д��AE��BF��������ϵ��������д�����̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com