
 如图,∠1+∠2=180°,∠A=∠C,BC平分∠EBD
如图,∠1+∠2=180°,∠A=∠C,BC平分∠EBD分析 (1)根据同角的余角相等,可得∠BDC=∠1,进而得出AE∥CP;
(2)根据AE∥CP,可得∠C+∠ABC=180°,再根据∠A=∠C,可得∠A+∠ABC=180°,进而得出AD∥BC;
(3)根据BC平分∠EBD,可得∠3=∠4,再根据平行线的性质,可得∠3=∠C=∠5,∠4=∠6,进而得到∠5=∠6,即DA平分∠BDP.
解答 解:(1)AE与CP平行.
∵∠1+∠2=180°,∠2+∠CDB=180°,
∴∠BDC=∠1,
∴AE∥CP;
(2)AD与BC平行.
∵AE∥CP,
∴∠C+∠ABC=180°,
又∵∠A=∠C,
∴∠A+∠ABC=180°,
∴AD∥BC;
(3)DA平分∠BDP.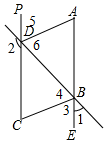
如图所示,∵BC平分∠EBD,
∴∠3=∠4,
∵AD∥BC,AB∥CD,
∠3=∠C=∠5,∠4=∠6,
∴∠5=∠6,
∴DA平分∠BDP.
点评 本题主要考查了平行线的性质与判定的综合运用,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在长为70米,宽为40米的长方形空地中,张老板想在上面修建焯天茶餐厅和子欣西餐厅,两所餐厅的四周铺上等宽的小路隔开,如果小路的面积占总面积的八分之一,求小路的宽度是多少?
如图,在长为70米,宽为40米的长方形空地中,张老板想在上面修建焯天茶餐厅和子欣西餐厅,两所餐厅的四周铺上等宽的小路隔开,如果小路的面积占总面积的八分之一,求小路的宽度是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
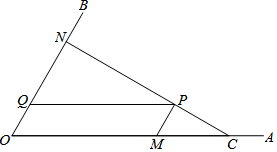 如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
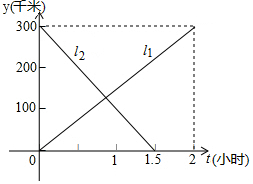 厦深铁路开通后,直线l1与l2分别表示从深圳北开往潮阳站的动车和从潮阳站开往深圳的高铁,两车同时出发,设动车离深圳北的距离为y1(千米),高铁离深圳的距离为距离y2(千米),行驶时间为t(小时),与t的函数关系如图所示:
厦深铁路开通后,直线l1与l2分别表示从深圳北开往潮阳站的动车和从潮阳站开往深圳的高铁,两车同时出发,设动车离深圳北的距离为y1(千米),高铁离深圳的距离为距离y2(千米),行驶时间为t(小时),与t的函数关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
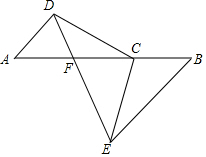 已知,如图:C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.
已知,如图:C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在⊙O中,AC是直径,CB是⊙O的切线,连接AB,AB与⊙O交于点D,连接OD,CD,E为BC上一点,连接DE,且CE=DE.
如图,已知在⊙O中,AC是直径,CB是⊙O的切线,连接AB,AB与⊙O交于点D,连接OD,CD,E为BC上一点,连接DE,且CE=DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com