
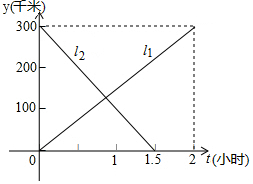
 厦深铁路开通后,直线l1与l2分别表示从深圳北开往潮阳站的动车和从潮阳站开往深圳的高铁,两车同时出发,设动车离深圳北的距离为y1(千米),高铁离深圳的距离为距离y2(千米),行驶时间为t(小时),与t的函数关系如图所示:
厦深铁路开通后,直线l1与l2分别表示从深圳北开往潮阳站的动车和从潮阳站开往深圳的高铁,两车同时出发,设动车离深圳北的距离为y1(千米),高铁离深圳的距离为距离y2(千米),行驶时间为t(小时),与t的函数关系如图所示:分析 (1)根据题意和函数图象中的数据可以求得高铁的速度;
(2)根据题意和函数图象中的数据可以求得动车的速度;
(3)根据函数图象中的数据可以分别求得高铁和动车对应的函数解析式,从而可以解答本题;
(4)根据(3)中的函数解析式,令它们的差的绝对值等于50即可解答本题.
解答 解:(1)由题意可得,
高铁的速度为:300÷1.5=200km/h,
故答案为:200;
(2)由题意可得,
动车的速度为:300÷2=150km/h,
故答案为:150;
(3)设动车对应的函数解析式为:y1=kx,
则2k=300,得k=150,
∴动车对应的函数解析式为:y1=150x,
高铁对应的函数解析式为:y2=ax+b,
$\left\{\begin{array}{l}{b=300}\\{1.5a+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{a=-200}\\{b=300}\end{array}\right.$,
即高铁对应的函数解析式为:y2=-200x+300,
则$\left\{\begin{array}{l}{y=150x}\\{y=-200x+300}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{6}{7}}\\{y=\frac{900}{7}}\end{array}\right.$,
即动车出发$\frac{6}{7}$小时与高铁相遇;
(4)由题意可得,
|150x-(-200x+300)|=50,
解得,x1=$\frac{5}{7}$,x2=1,
即两车出发$\frac{5}{7}$小时或1小时时相距50千米.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式,利用函数的性质和数形结合的思想解答问题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 cm或6 cm | B. | 6 cm | C. | 12 cm | D. | 12 cm或6 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠1+∠2=180°,∠A=∠C,BC平分∠EBD
如图,∠1+∠2=180°,∠A=∠C,BC平分∠EBD查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com