
ЁОЬтФПЁПФГСжвЕВПУХвЊПМВьФГгзУчЕФГЩЛюТЪЃЌгкЪЧНјааСЫЪдбщЃЌЯТБэжаМЧТМСЫетжжгзУчдквЛЖЈЬѕМўЯТвЦжВЕФГЩЛюЧщПіЃЌдђЯТСаЫЕЗЈВЛе§ШЗЕФЪЧЃЈ ЃЉ
вЦжВзмЪ§ | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
ГЩЛюЪ§ | 369 | 1335 | 3203 | 6335 | 8073 | 12628 |
ГЩЛюЕФЦЕТЪ | 0923 | 0.890 | 0915 | 0.905 | 0.897 | 0.902 |
A.гЩДЫЙРМЦетжжгзУчдкДЫЬѕМўЯТГЩЛюЕФИХТЪдМЮЊ0.9
B.ШчЙћдкДЫЬѕМўЯТдйвЦжВетжжгзУч20000жъЃЌдђБиЖЈГЩЛю18000жъ
C.ПЩвдгУЪдбщДЮЪ§РлМЦзюЖрЪБЕФЦЕТЪзїЮЊИХТЪЕФЙРМЦжЕ
D.дкДѓСПжиИДЪдбщжаЃЌЫцзХЪдбщДЮЪ§ЕФдіМгЃЌгзУчГЩЛюЕФЦЕТЪЛсдНРДдНЮШЖЈЃЌвђДЫПЩвдгУЦЕТЪЙРМЦИХТЪ
ЁОД№АИЁПB
ЁОНтЮіЁП
ДѓСПжиИДЪдбщЪБЃЌЪТМўЗЂЩњЕФЦЕТЪдкФГИіЙЬЖЈЮЛжУзѓгвАкЖЏЃЌВЂЧвАкЖЏЕФЗљЖШдНРДдНаЁЃЌИљОнетИіЦЕТЪЮШЖЈадЖЈРэЃЌПЩвдгУЦЕТЪЕФМЏжаЧїЪЦРДЙРМЦИХТЪЃЌетИіЙЬЖЈЕФНќЫЦжЕОЭЪЧетИіЪТМўЕФИХТЪМДПЩЕУЕНД№АИЃЎ
НтЃКгЩДЫЙРМЦетжжгзУчдкДЫЬѕМўЯТГЩЛюЕФИХТЪдМЮЊ0.9ЃЌЙЪAбЁЯюе§ШЗЃЛ
ШчЙћдкДЫЬѕМўЯТдйвЦжВетжжгзУч20000жъЃЌдђДѓдМГЩЛю18000жъЃЌЙЪBбЁЯюДэЮѓЃЛ
ПЩвдгУЪдбщДЮЪ§РлМЦзюЖрЪБЕФЦЕТЪзїЮЊИХТЪЕФЙРМЦжЕЃЌЙЪCбЁЯюе§ШЗЃЛ
дкДѓСПжиИДЪдбщжаЃЌЫцзХЪдбщДЮЪ§ЕФдіМгЃЌгзУчГЩЛюЕФЦЕТЪЛсдНРДдНЮШЖЈЃЌвђДЫПЩвдгУЦЕТЪЙРМЦИХТЪЃЌЙЪDбЁЯюе§ШЗ.
ЙЪбЁЃКBЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгЩСНИіПЩвдздгЩзЊЖЏЕФзЊХЬЁЂУПИізЊХЬБЛЗжГЩШчЭМЫљЪОЕФМИИіЩШаЮЁЂгЮЯЗепЭЌЪБзЊЖЏСНИізЊХЬЃЌШчЙћвЛИізЊХЬзЊГіСЫКьЩЋЃЌСэвЛзЊХЬзЊГіСЫРЖЩЋЃЌгЮЯЗепОЭХфГЩСЫзЯЩЋЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
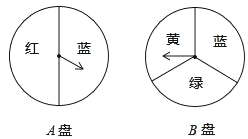
A. СНИізЊХЬзЊГіРЖЩЋЕФИХТЪвЛбљДѓ
B. ШчЙћAзЊХЬзЊГіСЫРЖЩЋЃЌФЧУДBзЊХЬзЊГіРЖЩЋЕФПЩФмадБфаЁСЫ
C. ЯШзЊЖЏA зЊХЬдйзЊЖЏB зЊХЬКЭЭЌЪБзЊЖЏСНИізЊХЬЃЌгЮЯЗепХфГЩзЯЩЋЕФИХТЪВЛЭЌ
D. гЮЯЗепХфГЩзЯЩЋЕФИХТЪЮЊ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁОгЊAжжЦЗХЦЕФЭцОпЃЌЙКНјЪБЕФЕЅМлЪЧ30дЊЃЌИљОнЪаГЁЕїВщЃКдквЛЖЮЪБМфФкЃЌЯњЪлЕЅМлЪЧ40дЊЪБЃЌЯњЪлСПЪЧ600МўЃЌЖјЯњЪлЕЅМлУПеЧ1дЊЃЌОЭЛсЩйЪлГі10МўЭцОпЃЎ
ЃЈ1ЃЉВЛЗСЩшИУжжЦЗХЦЭцОпЕФЯњЪлЕЅМлЮЊxдЊЃЈxЃО40ЃЉЃЌЧыгУКЌxЕФДњЪ§ЪНБэЪОИУЭцОпЕФЯњЪлСП.
ЃЈ2ЃЉШєЭцОпГЇЙцЖЈИУЦЗХЦЭцОпЯњЪлЕЅМлВЛЕЭгк44дЊЃЌЧвЩЬГЁвЊЭъГЩВЛЩйгк450МўЕФЯњЪлШЮЮёЃЌЧѓЩЬГЁЯњЪлИУЦЗХЦЭцОпЛёЕУЕФзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉИУЩЬГЁМЦЛЎНЋЃЈ2ЃЉжаЫљЕУЕФРћШѓЕФвЛВПЗжзЪН№ВЩЙКвЛХњBжжЭцОпВЂзЊЪжГіЪлЃЌИљОнЪаГЁЕїВщВЂзМБИСНжжЗНАИЃЌЗНАИЂйЃКШчЙћдТГѕГіЪлЃЌПЩЛёРћ15%ЃЌВЂПЩгУБОКЭРћдйЭЖзЪCжжЭцОпЃЌЕНдТФЉгжПЩЛёРћ10%ЃЛЗНАИЂкЃКШчЙћжЛЕНдТФЉГіЪлПЩжБНгЛёРћ30%ЃЌЕЋвЊСэжЇИЖВжПтБЃЙмЗб350дЊЃЌЧыЮЪЩЬГЁШчКЮЪЙгУетБЪзЪН№ЃЌВЩгУФФжжЗНАИЛёРћНЯЖрЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌНЋе§ЗНаЮ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() КѓЕУЕНе§ЗНаЮ
КѓЕУЕНе§ЗНаЮ![]() ЃЌвРДЫЗНЪНЃЌШЦЕу
ЃЌвРДЫЗНЪНЃЌШЦЕу![]() СЌаја§зЊ2019ДЮЕУЕНе§ЗНаЮ
СЌаја§зЊ2019ДЮЕУЕНе§ЗНаЮ![]() ЃЌШчЙћЕу
ЃЌШчЙћЕу![]() ЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌФЧУДЕу
ЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌФЧУДЕу![]() ЕФзјБъЮЊ________ЃЎ
ЕФзјБъЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЃЌдђОЙ§
ЃЌдђОЙ§![]() Ш§ЕуЕФдВЛЁЫљдкдВЕФдВаФ
Ш§ЕуЕФдВЛЁЫљдкдВЕФдВаФ![]() ЕФзјБъЮЊ__________ЃЛЕу
ЕФзјБъЮЊ__________ЃЛЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌжБЯп
ЃЌжБЯп![]() гы
гы![]() ЕФЮЛжУЙиЯЕЪЧ___________ЃЎ
ЕФЮЛжУЙиЯЕЪЧ___________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбДЦкЕНРДЃЌЩНКщБЉЗЂЃЎЯТБэМЧТМСЫФГЫЎПт![]() ФкЫЎЮЛЕФБфЛЏЧщПіЃЌЦфжа
ФкЫЎЮЛЕФБфЛЏЧщПіЃЌЦфжа![]() БэЪОЪБМф(ЕЅЮЛЃК
БэЪОЪБМф(ЕЅЮЛЃК![]() )ЃЌ
)ЃЌ![]() БэЪОЫЎЮЛИпЖШ(ЕЅЮЛЃК
БэЪОЫЎЮЛИпЖШ(ЕЅЮЛЃК![]() )ЃЌЕБ
)ЃЌЕБ![]() ЪБЃЌДяЕНОЏНфЫЎЮЛЃЌПЊЪМПЊеЂЗХЫЎЃЎ
ЪБЃЌДяЕНОЏНфЫЎЮЛЃЌПЊЪМПЊеЂЗХЫЎЃЎ
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 14 | 15 | 16 | 17 | 18 | 14.4 | 12 | 10.3 | 9 | 8 | 7.2 |

(1)дкИјГіЕФЦНУцжБНЧзјБъЯЕжаЃЌИљОнБэИёжаЕФЪ§ОнУшГіЯргІЕФЕуЃЎ
(2)ЧыЗжБ№ЧѓГіПЊеЂЗХЫЎЧАКЭЗХЫЎКѓзюЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪНЃЎ
(3)ОнЙРМЦЃЌПЊеЂЗХЫЎКѓЃЌЫЎЮЛЕФетжжБфЛЏЙцТЩЛЙЛсГжајвЛЖЮЪБМфЃЌдЄВтКЮЪБЫЎЮЛДяЕН![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧАыОЖЮЊ1ЕФЁбOЕФжБОЖЃЌЕуCдкЁбOЩЯЃЌЁЯCABЃН30ЁуЃЌDЮЊСгЛЁCBЕФжаЕуЃЌЕуPЪЧжБОЖABЩЯвЛИіЖЏЕуЃЌдђPC+PDЕФзюаЁжЕЮЊЃЈ ЃЉ
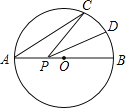
A.1B.2C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЃЌAЃЈ2![]() ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ1ЃЉЃЌШєPЮЊЯпЖЮOAЩЯвЛЖЏЕуЃЌдђCP+
ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ1ЃЉЃЌШєPЮЊЯпЖЮOAЩЯвЛЖЏЕуЃЌдђCP+![]() APЕФзюаЁжЕЮЊ_____ЃЎ
APЕФзюаЁжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮAOBCЗХжУдкЦНУцжБНЧзјБъЯЕxOyжаЃЌБпOAдкyжсЕФе§АыжсЩЯЃЌБпOBдкxжсЕФе§АыжсЩЯЃЌХзЮяЯпЕФЖЅЕуЮЊFЃЌЖдГЦжсНЛACгкЕуEЃЌЧвХзЮяЯпОЙ§ЕуAЃЈ0ЃЌ2ЃЉЃЌЕуCЃЌЕуDЃЈ3ЃЌ0ЃЉЃЎЁЯAOBЕФЦНЗжЯпЪЧOEЃЌНЛХзЮяЯпЖдГЦжсзѓВргкЕуHЃЌСЌНгHFЃЎ
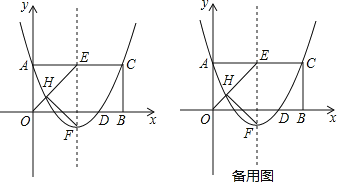
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкxжсЩЯгаЖЏЕуMЃЌЯпЖЮBCЩЯгаЖЏЕуNЃЌЧѓЫФБпаЮEAMNЕФжмГЄЕФзюаЁжЕЃЛ
ЃЈ3ЃЉИУХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЫФБпаЮEHFPЮЊЦНааЫФБпаЮЃПШчЙћДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com