
分析 根据旋转的性质,可得AB与A′B的关系,根据全等三角形的判定与性质,可得BC,A′C的长,根据等腰三角形的性质,可得AD即为所求的直线,根据中点坐标公式,可得D点坐标,根据待定系数法,可得答案.
解答 解:如图,作BD⊥AA′于D.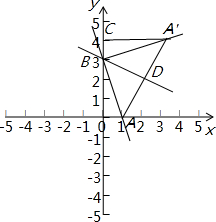 ,
,
当x=0时,y=3即B(0,3),
当y=0时,-3x+3=0,解得x=1,即A(1,0);
将l1绕B点逆时针旋转90°,则A点与A′对应,
作A′C⊥y轴与C点,
在△AOB和△BCA′中,
$\left\{\begin{array}{l}{∠ABO=∠BCA′}\\{∠AOB=∠BCA′}\\{AB=A′B}\end{array}\right.$,
△AOB≌△BCA′(AAS),
BC=AO=1,A′C=OB=3,
OC=1+3=4,
即A′(3,4).
∠ABD=∠A′BD=45°,
AD=A′D,
D(2,2).
设BD的解析式为y=kx+b,
将B,D点坐标代入,得
$\left\{\begin{array}{l}{b=3}\\{2k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$.
BD的解析式为y=-$\frac{1}{2}$x+3,
即l2的解析式y=-$\frac{1}{2}$x+3,.
点评 本题考查了一次函数图象与几何变换,利用旋转直线绕B点旋转90°得出A的对应点A′的坐标是解题关键,又利用了中点坐标公式得出D点坐标,待定系数法求函数解析式.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
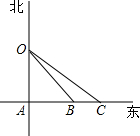 如图,有A、B、C三个村庄,A庄在某市的市中心正南方40km处,B、C两个村庄在A庄的正东方向上,且距A庄分别为30km和35km,该市中心有一座信息发射塔(即O点),覆盖半径为50km,问三个村庄A、B、C是否能收到该塔发出的信息.
如图,有A、B、C三个村庄,A庄在某市的市中心正南方40km处,B、C两个村庄在A庄的正东方向上,且距A庄分别为30km和35km,该市中心有一座信息发射塔(即O点),覆盖半径为50km,问三个村庄A、B、C是否能收到该塔发出的信息.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com