
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径 
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB= ![]() ,AE=4,求CD.
,AE=4,求CD.
【答案】
(1)结论:BC与⊙O相切.
证明:如图连接OD.
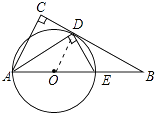
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠CAB,
∴∠CAD=∠DAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∵AC⊥BC,
∴OD⊥BC.
∴BC是⊙O的切线
(2)证明:∵BC是⊙O切线,
∴∠ODB=90°,
∴∠BDE+∠ODE=90°,
∵AE是直径,
∴∠ADE=90°,
∴∠DAE+∠AED=90°,
∵OD=OE,
∴∠ODE=∠OED,
∴∠BDE=∠DAB,
∵∠B=∠B,
∴△ABD∽△DBE
(3)解:在Rt△ODB中,∵cosB= ![]() =
= ![]() ,设BD=2
,设BD=2 ![]() k,OB=3k,
k,OB=3k,
∵OD2+BD2=OB2,
∴4+8k2=9k2,
∴k=2,
∴BO=6,BD=4 ![]() ,
,
∵DO∥AC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CD= ![]()
【解析】(1)结论:BC与⊙O相切,连接OD只要证明OD∥AC即可.(2)欲证明△ABD∽△DBE,只要证明∠BDE=∠DAB即可.(3)在Rt△ODB中,由cosB= ![]() =
= ![]() ,设BD=2
,设BD=2 ![]() k,OB=3k,利用勾股定理列出方程求出k,再利用DO∥AC,得
k,OB=3k,利用勾股定理列出方程求出k,再利用DO∥AC,得 ![]() =
= ![]() 列出方程即可解决问题.
列出方程即可解决问题.


科目:初中数学 来源: 题型:
【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本,小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会表现突出的同学,要求笔记本数不少于钢笔数.请问:有多少购买方案?请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了拉动内需,全国各地汽车购置税补贴活动正式开始.重庆长安汽车经销商在出台前一个月共售出长安SUV汽车CS35的手动型和自动型共960台,政策出台后的第一月售出这两种型号的汽车共1228台,其中手动型和自动型汽车的销售量分别比政策出台前一个月增长30%和25%.
(1)在政策出台前一个月,销售的手动型和自动型汽车分别为多少台?
(2)若手动型汽车每台价格为8万元,自动型汽车每台价格为9万元.根据汽车补贴政策,政府按每台汽车价格的5%给购买汽车的用户补贴,购车人需要交纳车辆购置各种税费杂费路桥保险等为每台汽车价格的22%,问政策出台后的第一个月,政府对这l228台汽车用户共补贴了多少万元?客户实际需要花多少钱才能够买一辆自动型的CS35汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
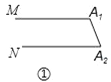
【题目】下列各图中的MA1与NAn平行.
(1)图①中的∠A1+∠A2=______度,
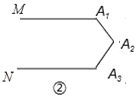
图②中的∠A1+∠A2+∠A3=______度,
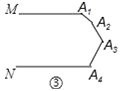
图③中的∠A1+∠A2+∠A3+∠A4=______度,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10=______度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An=______.
(3)证明图②中的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:

对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A. 甲运动员得分的极差大于乙运动员得分的极差
B. 甲运动员得分的中位数大于乙运动员得分的中位数
C. 甲运动员得分的平均数大于乙运动员得分的平均数
D. 甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y= ![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC , 记S=S四边形MAOC﹣S△BOC , 求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2 , 点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据条件画图,并回答问题:
(1)画一个锐角△ABC(三边均不相等);
(2)画出BC边上的中线AE和高AD;
(3)写出所有以AD为高的三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD中,E为AD的中点,CE的延长线交BA的延长线于点E.
(1)试说明线段CD与FA相等的理由;
(2)若使∠F=∠BCF,□ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com