
【题目】如图甲是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长方形,再按图乙围成一个较大的正方形.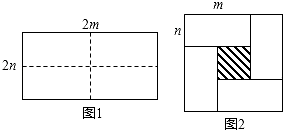
(1)请用两种方法表示图中阴影部分面积(只需表示,不必化简);
(2)比较(1)两种结果,你能得到怎样的等量关系?
请你用(2)中得到等量关系解决下面问题:如果m﹣n=5,mn=14,求m+n的值.
【答案】
(1)解:方法一:∵大正方形的面积为(m+n)2,四个小长方形的面积和为4mn,
∴中间阴影部分的面积为(m+n)2﹣4mn.
方法二:∵中间小正方形的边长为m﹣n,∴其面积为(m﹣n)2
(2)解:(m+n)2﹣4mn=(m﹣n)2.
∵m﹣n=5,mn=14,
∴(m+n)2﹣4×14=52,得m+n=9或m+n=﹣9(舍),
故m+n的值为9
【解析】(1)由图2的面积减去图一的面积可得阴影部分面积为(m+n)2﹣4mn;单独看图2易得阴影部分小正方形边长为m-n,可得面积为(m﹣n)2;
(2)由乘法公式易得(m+n)2﹣4mn=(m﹣n)2即两种结果相等;将m﹣n=5,mn=14带入易得m+n的值为9(边长之和为正数,所以-9舍去)


科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文艺团体为“希望工程”募捐组织了一场义演,共售出2000张票,筹得票款13600元.已知学生票5元/张,成人票8元/张,问成人票与学生票各售出多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
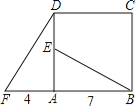
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com