
分析 【现学现用】模仿例题,利用配方法可得y=x+$\frac{1}{x}$=($\sqrt{x}$-$\frac{1}{\sqrt{x}}$)2+2,由此即可解决问题;
【拓展应用】(1)当v=100时,kv2=1,k=$\frac{1}{10000}$,可得y=$\frac{{v}^{2}}{10000}$+4(0<v≤300);
(2)由(1)可知y=$\frac{{v}^{2}}{10000}$+4,可得z=($\frac{{v}^{2}}{10000}$+4)•$\frac{400}{v}$=$\frac{v}{25}$+$\frac{1600}{v}$=$\frac{1}{25}$($\sqrt{v}$-$\frac{200}{\sqrt{v}}$)2+16≥16,由此即可解决问题;
解答 解:【现学现用】∵y=x+$\frac{1}{x}$=($\sqrt{x}$-$\frac{1}{\sqrt{x}}$)2+2,
∴当$\sqrt{x}$=$\frac{1}{\sqrt{x}}$时,y有最大值2,
∴x=1时,y有最大值2,
故答案为1,大,2.
【拓展应用】(1)∵当v=100时,kv2=1,k=$\frac{1}{10000}$,
∴y=$\frac{{v}^{2}}{10000}$+4(0<v≤300).
(2)由(1)可知y=$\frac{{v}^{2}}{10000}$+4,
∴z=($\frac{{v}^{2}}{10000}$+4)•$\frac{400}{v}$=$\frac{v}{25}$+$\frac{1600}{v}$=$\frac{1}{25}$($\sqrt{v}$-$\frac{200}{\sqrt{v}}$)2+16≥16,
∴当$\sqrt{v}$=$\frac{200}{\sqrt{v}}$时,即v=200时,z有最小值16,
∴为了使全程运行成本z最低,高铁行驶的速度应为200千米/小时.
点评 本题考查反比例函数综合题、配方法、非负数的性质等知识,解题的关键是学会模仿例题解决问题,灵活运用配方法解决问题,属于中考创新题目.


科目:初中数学 来源: 题型:解答题
 已知:一次函数y=2x+4
已知:一次函数y=2x+4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
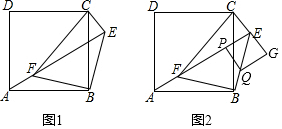
 如图,四边形ABCD中,AB=AD,∠ABC=∠ADC.
如图,四边形ABCD中,AB=AD,∠ABC=∠ADC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
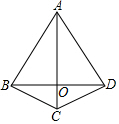
 如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
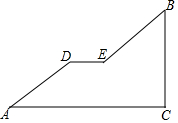 如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
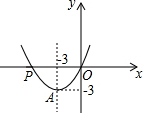 已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.
已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
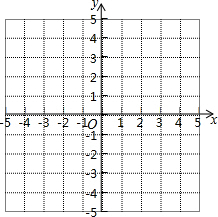
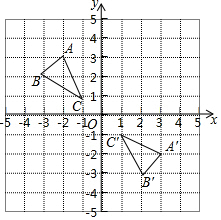 如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3)、B(-3,2)、C(-1,1)
如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3)、B(-3,2)、C(-1,1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com