练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

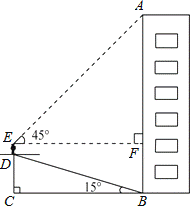
    小华为了测量楼房AB的高度，他从楼底的B处沿着斜坡向上行走20m，到达坡顶D处．已知斜坡的坡角为15°．（以下计算结果精确到0.1m）

    （1）求小华此时与地面的垂直距离CD的值；

    （2）小华的身高ED是1.6m，他站在坡顶看楼顶A处的仰角为45°，求楼房AB的高度．

    　

     


           解：（1）在Rt△BCD中，∠CBD=15°，BD=20，

    ∴CD=BD•sin15°，

    ∴CD=5.2（m）．

    答：小华与地面的垂直距离CD的值是5.2m；

    （2）在Rt△AFE中，

    ∵∠AEF=45°，

    ∴AF=EF=BC，

    由（1）知，BC=BD•cos15°≈19.3（m），

    ∴AB=AF+DE+CD=19.3+1.6+5.2=26.1（m）．

    答：楼房AB的高度是26.1m．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，直线y=﹣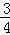x+3与x轴交于点C，与y轴交于点B，抛物线y=ax2+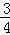x+c经过B、C两点．

    （1）求抛物线的解析式；

    （2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC面积的最大值？

    （3）在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AD是⊙O的直径，弦于E，，则_______。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点E，F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加的一个条件是（　　）

    　   A．∠A=∠C         B． ∠D=∠B               C．                             AD∥BC   D． DF∥BE

    　

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    .小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上，此时，光盘与AB，CD分别相切于点N，M．现从如图所示的位置开始，将光盘在直尺边上沿着CD向右滚动到再次与AB相切时，光盘的圆心经过的距离是　　　　　　．

    　

    　

     

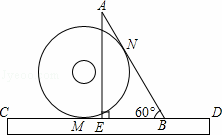
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．

    （1）求MP的值；

    （2）在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？

    （3）若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）

    　

    　


     

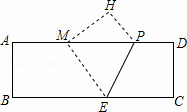
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，下列条件中，不能证明△ABC≌△DCB的是（　　）

    　 A． AB=DC，AC=DB B． AB=DC，∠ABC=∠DCB

    　 C． BO=CO，∠A=∠D D． AB=DC，∠A=∠D

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K，点O是线段BK的中点．

    （1）求证：△ADP≌△ECP；

    （2）若BP=n•PK，试求出n的值；

    （3）作BM丄AE于点M，作KN丄AE于点N，连结MO、NO，如图2所示，请证明△MON是等腰三角形，并直接写出∠MON的度数．

     

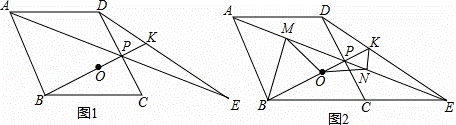
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．分解因式：ab2﹣9a=　　

     

    查看答案和解析>>

    同步练习册答案