
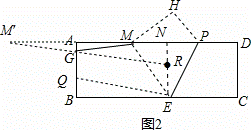
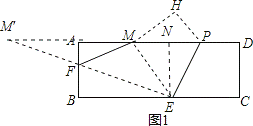
如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
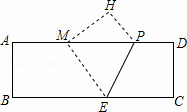
解:(1)∵四边形ABCD为矩形,
∴CD=AB=4,∠D=90°,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,
∴PD=PH=3,CD=MH=4,∠H=∠D=90°,
∴MP=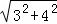 =5;
=5;
(2)如图1,作点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,
∵AM=AD﹣MP﹣PD=12﹣5﹣3=4,
∴AM=AM′=4,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,
∴∠CEP=∠MEP,
而∠CEP=∠MPE,
∴∠MEP=∠MPE,
∴ME=MP=5,
在Rt△ENM中,MN=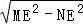 =
=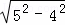 =3,
=3,
∴NM′=11,
∵AF∥ME,
∴△AFM′∽△NEM′,
∴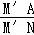 =
=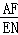 ,即
,即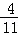 =
=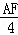 ,解得AF=
,解得AF=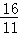 ,
,
即AF=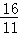 时,△MEF的周长最小;
时,△MEF的周长最小;
(3)如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,
∵ER=GQ,ER∥GQ,
∴四边形ERGQ是平行四边形,
∴QE=GR,
∵GM=GM′,
∴MG+QE=GM′+GR=M′R,此时MG+EQ最小,四边形MEQG的周长最小,
在Rt△M′RN中,NR=4﹣2=2,
M′R=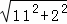 =5
=5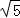 ,
,
∵ME=5,GQ=2,
∴四边形MEQG的最小周长值是7+5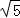 .
.


科目:初中数学 来源: 题型:
下列事件是必然事件的为( )
A.明天太阳从西方升起
B.掷一枚硬币,正面朝上
C.打开电视机,正在播放 “河池新闻”
D.任意一个三角形,它的内角和等于180°
查看答案和解析>>
科目:初中数学 来源: 题型:
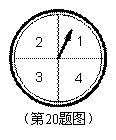
某超市计划在“十周年”庆典当天开展购物抽奖活动,凡是当天在该超市购物的顾客,均有一次抽奖机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止指针所指扇形内的数为每次所得的数(若指针指在分界线时重转),当两次所得的数字之和为8时,返还现金20元;当两次所得的数字之和为7时,返还现金15元;当两次所得的数字之和为6时,返还现金10元。
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果。
(2)某顾客参加一次抽奖,能获得反还现金的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
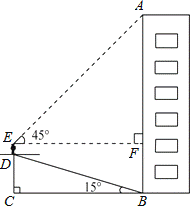
小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
(1)求小华此时与地面的垂直距离CD的值;
(2)小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )
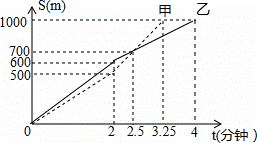
A. 甲、乙两人进行1000米赛跑
B. 甲先慢后快,乙先快后慢
C. 比赛到2分钟时,甲、乙两人跑过的路程相等
D. 甲先到达终点
查看答案和解析>>
科目:初中数学 来源: 题型:
每年的5月31日为世界无烟日,开展无烟日活动旨在提醒世人吸烟有害健康,呼吁全世界吸烟者主动放弃吸烟,全世界每年因吸烟而引发疾病死亡的人数大约为5400000人,数据5400000人用科学记数法表示为 人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com