
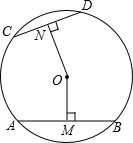
 如图所示,在⊙O中,AB,CD是两条弦,且AB>CD,OM⊥AB于点M,ON⊥CD于点N,请你猜想0M与0N的大小关系,并说明理由.
如图所示,在⊙O中,AB,CD是两条弦,且AB>CD,OM⊥AB于点M,ON⊥CD于点N,请你猜想0M与0N的大小关系,并说明理由. 科目:初中数学 来源: 题型:解答题
| 税级 | 全月应纳所得额 | 税率/% |
| 1 | 不超过1500元的部分 | 3 |
| 2 | 超过1500元至4500元的部分 | 10 |
| 3 | 超过4500元至9000元的部分 | 20 |
| … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $y=-\frac{x}{2}$ | B. | y=kx+b(k、b为常数) | C. | y=c(c为常数) | D. | $y=\frac{2}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元/台) | 60 | 55 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$)-2=-9 | B. | ($\frac{1}{3}$)-2=$\sqrt{3}$ | C. | ($\frac{1}{3}$)${\;}^{\frac{1}{2}}$=$\sqrt{3}$ | D. | 3${\;}^{-\frac{1}{2}}$=$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com