
| ˰�� | ȫ��Ӧ�����ö� | ˰��/% |
| 1 | ������1500Ԫ�IJ��� | 3 |
| 2 | ����1500Ԫ��4500Ԫ�IJ��� | 10 |
| 3 | ����4500Ԫ��9000Ԫ�IJ��� | 20 |
| �� | �� | �� |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a4•a3=a12 | B�� | a3•b3=��ab��3 | C�� | ��a3��2=a5 | D�� | a6��a3=a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{6}$ | B�� | $\frac{5}{18}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
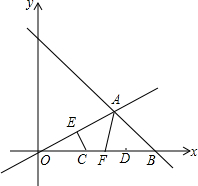 ��ͼ��ֱ��l1��y=-x+6��x�ύ�ڵ�B����ֱ��l2��y=$\frac{1}{2}$x�����A����EΪ�߶�OA���е㣬��FΪ�߶�CD���е㣬��Ϊ2�Ķ��߶�CD���˵�C��ԭ��O��ʼ�����߶�OB����ÿ��1����λ���ٶ����B�˶������˵�D�����Bʱ�˶�ֹͣ�����˶�ʱ��Ϊt�룬��ô��t=$\frac{7}{3}$��ʱ���ı���AECF���ܳ���С��
��ͼ��ֱ��l1��y=-x+6��x�ύ�ڵ�B����ֱ��l2��y=$\frac{1}{2}$x�����A����EΪ�߶�OA���е㣬��FΪ�߶�CD���е㣬��Ϊ2�Ķ��߶�CD���˵�C��ԭ��O��ʼ�����߶�OB����ÿ��1����λ���ٶ����B�˶������˵�D�����Bʱ�˶�ֹͣ�����˶�ʱ��Ϊt�룬��ô��t=$\frac{7}{3}$��ʱ���ı���AECF���ܳ���С���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
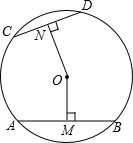 ��ͼ��ʾ���ڡ�O�У�AB��CD�������ң���AB��CD��OM��AB�ڵ�M��ON��CD�ڵ�N���������0M��0N�Ĵ�С��ϵ����˵�����ɣ�
��ͼ��ʾ���ڡ�O�У�AB��CD�������ң���AB��CD��OM��AB�ڵ�M��ON��CD�ڵ�N���������0M��0N�Ĵ�С��ϵ����˵�����ɣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com