
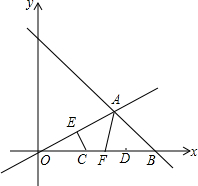
 如图,直线l1:y=-x+6与x轴交于点B,与直线l2:y=$\frac{1}{2}$x交与点A,点E为线段OA的中点,点F为线段CD的中点,长为2的动线段CD(端点C从原点O开始)在线段OB上以每秒1个单位的速度向点B运动,当端点D到达点B时运动停止.设运动时间为t秒,那么当t=$\frac{7}{3}$秒时,四边形AECF的周长最小.
如图,直线l1:y=-x+6与x轴交于点B,与直线l2:y=$\frac{1}{2}$x交与点A,点E为线段OA的中点,点F为线段CD的中点,长为2的动线段CD(端点C从原点O开始)在线段OB上以每秒1个单位的速度向点B运动,当端点D到达点B时运动停止.设运动时间为t秒,那么当t=$\frac{7}{3}$秒时,四边形AECF的周长最小. 分析 y=-x+6与y=$\frac{1}{2}$x联立,从而可解得A的坐标,根据点E是OA的中点,可得出点E的坐标,作CE关于x轴的对称线段,CE′,将CE′向右平移至FE″,当FE″与AF共线时四边形AECF的周长最小,然后求得AE″的直线解析式,将点F的坐标代入可求出t的值.
解答 解:如图,作CE关于x轴的对称线段CE′,将CE′向右平移至FE″.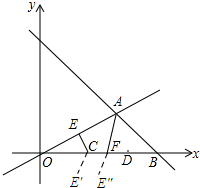
将y=-x+6与y=$\frac{1}{2}$x联立得:$\left\{\begin{array}{l}{y=-x+6}\\{y=\frac{1}{2}x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,即点A的坐标为(4,2),
∵点E是OA的中点,
∴点E的坐标为(2,1).
∵C(t,0),CD=2,点F是CD的中点,
∴CF=1,点F(t+1,0).
∵点E与点E′关于x轴对称,
∴点E′的坐标为(2,-1),CE=CE′.
由平行的性质可知:点E″的坐标为(3,-1),E″F=CE′=CE.
设过A(4,2),E″(3,-1)两点的直线表达式为y=kx+b,则$\left\{\begin{array}{l}{4k+b=2}\\{3k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=3}\\{b=-10}\end{array}\right.$,
∴直线AE″的表达式为:y=3x-10.
∵AE和CF的长度固定不变,
∴当EC+AF最短时,四边形AECF的周长最小.
∵EC+AF=FE″+AF,
∴当点A、E″F在一条直线上时,EC+AF有最小值.
将点F(t+1,0)代入y=3x-10得;3(t+1)-10=0.
解得:t=$\frac{7}{3}$.
∴当t=$\frac{7}{3}$时,四边形AECF的周长最小.
故答案为:$\frac{7}{3}$.
点评 本题考查了一次函数综合应用,涉及了动点问题、待定系数法求函数解析式、轴对称的性质、平行的性质,明确当点A、E″F在一条直线上时,四边形的周长最小是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
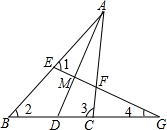 如图,在△ABC中,AD平分∠BAC,EG⊥AD,分别交AB、AD、AC于点E、M、F,交BC的延长线于点G,给出下列四个等式:①∠1=$\frac{1}{2}$(∠2+∠3);②∠1=$\frac{1}{2}$(∠3-∠2);③∠4=$\frac{1}{2}$(∠3-∠2);④∠4=$\frac{1}{2}$∠1.其中,正确的是①③(填序号).
如图,在△ABC中,AD平分∠BAC,EG⊥AD,分别交AB、AD、AC于点E、M、F,交BC的延长线于点G,给出下列四个等式:①∠1=$\frac{1}{2}$(∠2+∠3);②∠1=$\frac{1}{2}$(∠3-∠2);③∠4=$\frac{1}{2}$(∠3-∠2);④∠4=$\frac{1}{2}$∠1.其中,正确的是①③(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 税级 | 全月应纳所得额 | 税率/% |
| 1 | 不超过1500元的部分 | 3 |
| 2 | 超过1500元至4500元的部分 | 10 |
| 3 | 超过4500元至9000元的部分 | 20 |
| … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
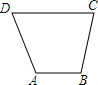 为迎接雨季的到来,某市决定对城边某条泄水沟进行清淤整理,水沟的截面为一梯形,如图所示,为保证泄水量,梯形面积规划为30m2,为了美观,要求AB=$\frac{1}{2}$CD,设AB的长为x m,沟深为y m.
为迎接雨季的到来,某市决定对城边某条泄水沟进行清淤整理,水沟的截面为一梯形,如图所示,为保证泄水量,梯形面积规划为30m2,为了美观,要求AB=$\frac{1}{2}$CD,设AB的长为x m,沟深为y m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com