
【题目】一个几何体的主视图、俯视图和左视图都是大小相同的圆,则这个几何体是 .
科目:初中数学 来源: 题型:
【题目】如果a=(-99)0 , b=(-0.1)-1 , c=(- ![]() )-2 , 那么a , b , c三数的大小为( )
)-2 , 那么a , b , c三数的大小为( )
A.a>b>c
B.c>a>b
C.a>c>b
D.
c>b>a |
查看答案和解析>>
科目:初中数学 来源: 题型:
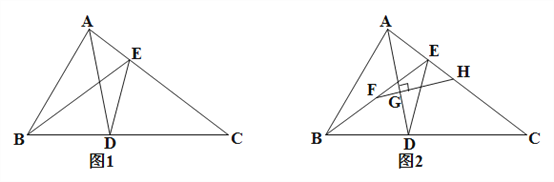
【题目】在ΔABC中点D为BC上一点,E为AC上一点,连接AD、BE、DE,已知BD=DE,AD=DC,∠ADB=∠CDE.
(1)如图1,若∠ACB=40°时,求∠BAC的度数.
(2)如图2,F是BE的中点,过点F作AD的垂线,分别交AD、AC于点G、H,求证:AH=CH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
【问题探究】
不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以先从特殊入手,通过试验、观察、类比、最后归纳、猜测得出结论.
【探究一】
(1)用3根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
此时,显然能搭成一种等腰三角形.
所以,当n=3时,m=1.
(2)用4根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形.
所以,当n=4时,m=0.
(3)用5根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形.
所以,当n=5时,m=1.
(4)用6根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形.
所以,当n=6时,m=1.
综上所述,可得:表①

【探究二】
(1)用7根相同的木棒搭一个三角形,能搭成多少种不同的三角形?
(仿照上述探究方法,写出解答过程,并将结果填在表②中)
(2)用8根、9根、10根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
表②

你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
【问题解决】:
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(设n分别等于4k﹣1,4k,4k+1,4k+2,其中k是正整数,把结果填在表③中)
表③

【问题应用】:
用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(写出解答过程),其中面积最大的等腰三角形每腰用了 根木棒.(只填结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com