
【题目】【问题提出】
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
【问题探究】
不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以先从特殊入手,通过试验、观察、类比、最后归纳、猜测得出结论.
【探究一】
(1)用3根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
此时,显然能搭成一种等腰三角形.
所以,当n=3时,m=1.
(2)用4根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形.
所以,当n=4时,m=0.
(3)用5根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形.
所以,当n=5时,m=1.
(4)用6根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形.
所以,当n=6时,m=1.
综上所述,可得:表①

【探究二】
(1)用7根相同的木棒搭一个三角形,能搭成多少种不同的三角形?
(仿照上述探究方法,写出解答过程,并将结果填在表②中)
(2)用8根、9根、10根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
表②

你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
【问题解决】:
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(设n分别等于4k﹣1,4k,4k+1,4k+2,其中k是正整数,把结果填在表③中)
表③

【问题应用】:
用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(写出解答过程),其中面积最大的等腰三角形每腰用了 根木棒.(只填结果)
【答案】【探究二】:2;1;2;2;【问题解决】:k;k﹣1;k;k;【问题应用】:672.
【解析】
试题分析:探究二:仿照探究一的方法进行分析即可;
问题解决:根据探究一、二的结果总结规律填表即可;
问题应用:根据规律进行计算求出m的值.
试题解析:(1)用7根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
此时,能搭成二种等腰三角形,即分成2根木棒、2根木棒和3根木棒,则能搭成一种等腰三角形
分成3根木棒、3根木棒和1根木棒,则能搭成一种等腰三角形
当n=7时,m=2.
(2)用8根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
分成2根木棒、2根木棒和4根木棒,则不能搭成一种等腰三角形,分成3根木棒、3根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=8时,m=1.
用9根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
分成3根木棒、3根木棒和3根木棒,则能搭成一种等腰三角形
分成4根木棒、4根木棒和1根木棒,则能搭成一种等腰三角形
所以,当n=9时,m=2.
用10根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
分成3根木棒、3根木棒和4根木棒,则能搭成一种等腰三角形
分成4根木棒、4根木棒和2根木棒,则能搭成一种等腰三角形
所以,当n=10时,m=2.
故答案为:2;1;2;2.
问题解决:由规律可知,答案为:k;k﹣1;k;k.
问题应用:2016÷4=504,504﹣1=503,当三角形是等边三角形时,面积最大,2016÷3=672,∴用2016根相同的木棒搭一个三角形,能搭成503种不同的等腰三角形,其中面积最大的等腰三角形每腰用672根木棒.


科目:初中数学 来源: 题型:
【题目】某市2013年参加中考的考生人数约为85000人,将85000用科学记数法表示为( )
A.8.5×104
B.8.5×105
C.0.85×104
D.0.85×105
查看答案和解析>>
科目:初中数学 来源: 题型:
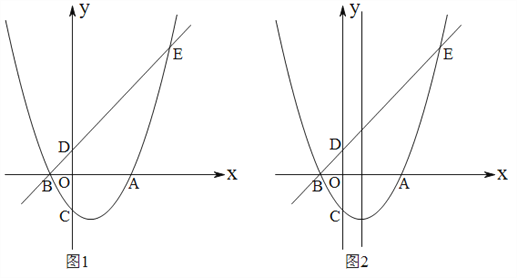
【题目】已知,如图1:抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,对称轴为直线
,对称轴为直线![]() ,且过点
,且过点![]() .
.
(1)求出抛物线的解析式及![]() 点坐标,
点坐标,
(2)点![]() ,
, ![]() ,作直线
,作直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的点,连接
下方抛物线上的点,连接![]() 、
、![]() ,求
,求![]() 的面积的最大值,并求出此时点
的面积的最大值,并求出此时点![]() 的坐标;
的坐标;
(3)点![]() 、
、![]() 是抛物线对称轴上的两点,且已知
是抛物线对称轴上的两点,且已知![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ,
, ![]() ),当
),当![]() 为何值时,四边形
为何值时,四边形![]() 周长最小?并求出四边形
周长最小?并求出四边形![]() 周长的最小值,请说明理由.
周长的最小值,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度是________ m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是多少?
(2)请你估计袋中红球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( ) 
A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com