
【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是多少?
(2)请你估计袋中红球接近多少个?
【答案】
(1)解:∵20×400=8000,
∴摸到红球的概率为: ![]() =0.75,
=0.75,
因为试验次数很大,大量试验时,频率接近于理论概率,
所以估计从袋中任意摸出一个球,恰好是红球的概率是0.75
(2)解:设袋中红球有x个,根据题意得:
![]() =0.75,
=0.75,
解得x=15,
经检验x=15是原方程的解.
∴估计袋中红球接近15个
【解析】求出总次数,根据红球出现的频数,求出红球出现的频率,即可用来估计红球出现的概率.
【考点精析】认真审题,首先需要了解用频率估计概率(在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率),还要掌握概率公式(一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n)的相关知识才是答题的关键.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积.
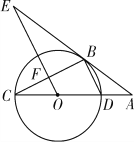
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式: a1=![]() =
=![]() ×(1
×(1![]() ) ;
) ;
第2个等式: a2=![]() =
=![]() ×(
×(![]()
![]() ) ;
) ;
第3个等式: a3=![]() =
=![]() ×(
×(![]()
![]() ) ;
) ;
第4个等式: a4=![]() =
=![]() ×(
×(![]()
![]() ) ;
) ;
…
请解答下列问题:
(1)按以上规律列出第6个等式: a6==.
(2)![]() 用含有 n 的代数式表示第 n 个等式: an==.(
用含有 n 的代数式表示第 n 个等式: an==.( ![]() 为正整数);
为正整数);
(3)求 a1+a2+a3+...+a100 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n﹣m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有6个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为40000人次,公园游戏场发放的福娃玩具为10000个.
(1)求参加一次这种游戏活动得到福娃玩具的概率;
(2)请你估计袋中白球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解光明中学学生平均每周的体育锻炼时间,小敏在校内随机调查了50名同学,统计并绘制了频数分布表(如下表)和扇形统计图(如图).
组别 | 锻炼时间(h/周) | 频数 |
A | 1.5≤t<3 | 1 |
B | 3≤t<4.5 | 2 |
C | 4.5≤t<6 | a |
D | 6≤t<7.5 | 20 |
E | 7.5≤t<9 | 15 |
F | t≥9 | b |

(1)a= , b= .
(2)在扇形统计图中,D组所占圆心角的度数为 .
(3)全校共有3000名学生,请你帮助小敏估计该校平均每周体育锻炼时间不少于6h的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
上课时李老师提出这样一个问题:对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,求a的取值范围.
小捷的思路是:原不等式等价于x2﹣2x﹣1>a,设函数y1=x2﹣2x﹣1,y2=a,画出两个函数的图象的示意图,于是原问题转化为函数y1的图象在y2的图象上方时a的取值范围.

请结合小捷的思路回答:
对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,则a的取值范围是 .
参考小捷思考问题的方法,解决问题:
关于x的方程x﹣4=![]() 在0<a<4范围内有两个解,求a的取值范围.
在0<a<4范围内有两个解,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com