
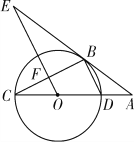
【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积.
【答案】(1)证明见解析;(2)10;(3)![]()
【解析】试题分析:(1)连接OB,利用已知条件和切线的性质证明:OE∥BD,即可证明:∠E=∠C;
(2)根据题意求出AB的长,然后根据平行线分线段定理,可求解;
(3)根据相似三角形的面积比等于相似比的平方可求解.
试题解析:(1)如解图,连接OB,
∵CD为⊙O的直径,
∴∠CBD=∠CBO+∠OBD=90°,
∵AB是⊙O的切线,
∴∠ABO=∠ABD+∠OBD=90°,
∴∠ABD=∠CBO.
∵OB、OC是⊙O的半径,
∴OB=OC,∴∠C=∠CBO.
∵OE∥BD,∴∠E=∠ABD,
∴∠E=∠C;
(2)∵⊙O的半径为3,AD=2,
∴AO=5,∴AB=4.
∵BD∥OE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BE=6,AE=6+4=10
(3)S△AOE=![]()
![]() =15,然后根据相似三角形面积比等于相似比的平方可得
=15,然后根据相似三角形面积比等于相似比的平方可得
S△ABC= ![]() S△AOE=
S△AOE=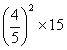 =
=![]()


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
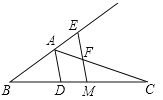
【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE=![]() (AB+AC).
(AB+AC).
查看答案和解析>>
科目:初中数学 来源: 题型:
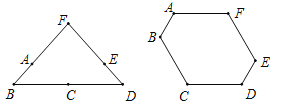
【题目】由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球.下列事件是必然事件的是( )
A.摸出的三个球中至少有一个球是黑球
B.摸出的三个球中至少有一个球是白球
C.摸出的三个球中至少有两个球是黑球
D.摸出的三个球中至少有两个球是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是多少?
(2)请你估计袋中红球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com