
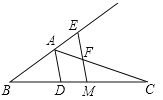
【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE=![]() (AB+AC).
(AB+AC).
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)欲证明AE=AF,只要证明∠AEF=∠AFE即可.
(2)作CG∥EM,交BA的延长线于G,先证明AC=AG,再证明BE=EG即可解决问题.
试题解析:(1)∵DA平分∠BAC,∴∠BAD=∠CAD,∵AD∥EM,∴∠BAD=∠AEF,∠CAD=∠AFE,∴∠AEF=∠AFE,∴AE=AF.
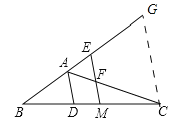
(2)作CG∥EM,交BA的延长线于G.
∵EF∥CG,∴∠G=∠AEF,∠ACG=∠AFE,∵∠AEF=∠AFE,∴∠G=∠ACG,∴AG=AC,∵BM=CM.EM∥CG,∴BE=EG,∴BE=![]() BG=
BG=![]() (BA+AG)=
(BA+AG)=![]() (AB+AC).
(AB+AC).


科目:初中数学 来源: 题型:
【题目】为了了解市民对“汕头市创建全国文明城市”的态度,某一天,小明等同学在本市的甲、乙和丙三个村的村民进行了一次随机调査,结果如图表:
村民态度 | 甲村 | 乙村 | 丙村 | 合计 |
关注 | 20 | 75 | 55 | 150 |
一般 | 23 | 5 | 17 | 45 |
不关心 | 57 | 20 | 28 | 105 |

(1)请将频数分布直方图补充完整;
(2)此次共调查了多少人?并求出一般在扇形统计图中所占圆心角的度数.
(3)用您学过的统计知识来说明哪个村的调査结果更能反映市民对“创文”的态度,请写出一句“创文”的宣传语.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算中,错误的是( )
A. 3a﹣2a=a B. ﹣2a(3a﹣1)=﹣6a2﹣1 C. ﹣8a2÷2a=﹣4a D. (a+3b)2=a2+6ab+9b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC是∠AOM的平分线,OD是∠BOM的平分线.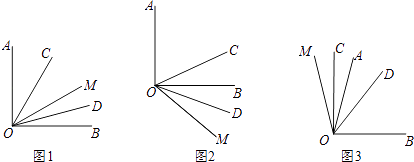
(1)如图1,若∠AOB=90°,∠AOM=60°,求∠COD的度数;
(2)如图2,若∠AOB=90°,∠AOM=130°,则∠COD=°;
(3)如图3,若∠AOB=m°,∠AOM=n°,则∠COD=°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上四个点A,B,C,D. 按要求完成下列问题: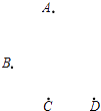
(1)①连接AC,BD;②画射线AB与直线CD相交于点E;
(2)用量角器度量∠AED的大小为(精确到度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
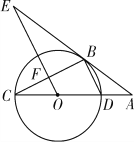
【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com