
【题目】如图,OC是∠AOM的平分线,OD是∠BOM的平分线.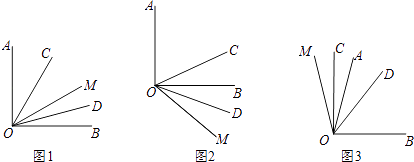
(1)如图1,若∠AOB=90°,∠AOM=60°,求∠COD的度数;
(2)如图2,若∠AOB=90°,∠AOM=130°,则∠COD=°;
(3)如图3,若∠AOB=m°,∠AOM=n°,则∠COD=°.
【答案】
(1)解:如图1,
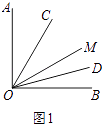
∵∠AOB=90°,∠AOM=60°,
∴∠BOM=∠AOB﹣∠AOM=90°﹣60°=30°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM= ![]() ∠AOM=
∠AOM= ![]() ×60°=30°,
×60°=30°,
∠DOM= ![]() ∠BOM=
∠BOM= ![]() ×30°=15°,
×30°=15°,
∴∠COD=∠COM+∠DOM=30°+15°=45°
(2)45
(3)![]() (m﹣n)°
(m﹣n)°
【解析】解:(2)如图2,
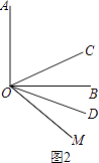
∵∠AOB=90°,∠AOM=130°,
∴∠BOM=∠AOM﹣∠AOB=130°﹣90°=40°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM= ![]() ∠AOM=
∠AOM= ![]() ×130°=65°,
×130°=65°,
∠DOM= ![]() ∠BOM=
∠BOM= ![]() ×40°=20°,
×40°=20°,
∴∠COD=∠COM﹣∠DOM=65°﹣20°=45°
所以答案是:45.
( 3 )如图3,
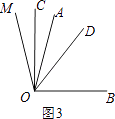
∵∠AOB=m°,∠AOM=n°,
∴∠BOM=∠AOB+∠AOM=m°+n°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM= ![]() ∠AOM=
∠AOM= ![]() ×n°=
×n°= ![]() n°,
n°,
∠DOM= ![]() ∠BOM=
∠BOM= ![]() m°,
m°,
∴∠COD=∠DOM﹣∠COM= ![]() m°﹣
m°﹣ ![]() n°=
n°= ![]() (m﹣n)°.
(m﹣n)°.
所以答案是: ![]() (m﹣n)°.
(m﹣n)°.
【考点精析】本题主要考查了角的平分线和角的运算的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题满分6分)一只不透明的袋子中装有1个白球、1个蓝球和2个红球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,摸出红球的概率为 ;
(2)从袋中随机摸出1个球(不放回)后,再从袋中余下的3个球中随机摸出1个球,球两次摸到的球颜色不相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
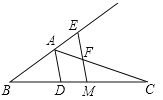
【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE=![]() (AB+AC).
(AB+AC).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com