练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：在△ABC中，若△ABC的三边a,b,c满足 a:b: c=5:12:13，判断△ABC的形状.

    【答案】直角三角形.

    【解析】

    由a:b: c=5:12:13，可设a=5x,b=12x,c=13x.则可得a2+b2=c2,再根据勾股定理的逆定理即可得到结果.

    解：∵a:b: c=5:12:13，

    ∴设a=5x,b=12x,c=13x.则

    a2+b2=（5x）2+(12x)2=25x2+144x2=169x2=(13x)2= c2

    ∴△ABC的形状是直角三角形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

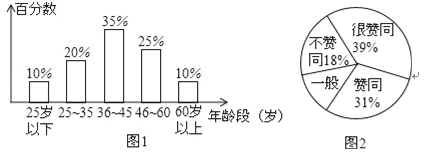
    【题目】据报载，在“百万家庭低碳行，垃圾分类要先行”活动中，某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查，并将调查结果分别绘成条形图（图1）、扇形图（图2）．

    （1）图2中所缺少的百分数是 ；

    （2）这次随机调查中，如果公民年龄的中位数是正整数，那么这个中位数所在年龄段是 ____ （填写年龄段）；

    （3）这次随机调查中，年龄段是“25岁以下”的公民中“不赞成”的有5名，它占“25岁以下”人数的百分数是 ___ ；

    （4）如果把所持态度中的“很赞同”和“赞同”统称为“支持”，那么这次被调查公民中“支持”的人有 ____名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当x取（ ）时，代数式3（2-x）和2（3+x）的值相等。

    A. 1 B. 2 C. -2 D. 0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数过（﹣2，4），（﹣4，4）两点．

    （1）求二次函数的解析式；

    （2）将沿x轴翻折，再向右平移2个单位，得到抛物线，直线y=m（m＞0）交于M、N两点，求线段MN的长度（用含m的代数式表示）；

    （3）在（2）的条件下，、交于A、B两点，如果直线y=m与、的图象形成的封闭曲线交于C、D两点（C在左侧），直线y=﹣m与、的图象形成的封闭曲线交于E、F两点（E在左侧），求证：四边形CEFD是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示的图像反映的过程是：甲乙两人同时从地出发,以各自的速度匀速向地行驶，甲先到地停留半小时后，按原路以另一速度匀速返回,直至与乙相遇.乙的速度为， 表示甲乙两人相距的距离， 表示乙行驶的时间.现有以下个结论：①、两地相距；②点的坐标为；③甲去时的速度为；④甲返回的速度是.以上个结论中正确的是_______________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小明所在教学楼的每层高度为3.5米，为了测量旗杆MN的高度，他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°，他在二楼窗台B处测得M的仰角为31°，已知每层楼的窗台离该层的地面高度均为1米，求旗杆MN的高度；（结果保留两位小数）

    （参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校要求八年级同学在课外活动中，必须在五项球类（篮球、足球、排球、羽毛球、乒乓球）活动中任选一项（只能选一项）参加训练，为了了解八年级学生参加球类活动的整体情况，现以八年级2班作为样本，对该班学生参加球类活动的情况进行统计，并绘制了如图所示的不完整统计表和扇形统计图：

    根据图中提供的信息，解答下列问题：

    （1）a= ，b= ；

    （2）该校八年级学生共有600人，则该年级参加足球活动的人数约 人；

    （3）该班参加乒乓球活动的5位同学中，有3位男同学（A，B，C）和2位女同学（D，E），现准备从中选取两名同学组成双打组合，用树状图或列表法求恰好选出一男一女组成混合双打组合的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为4的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的有 （写出所有正确结论的序号）

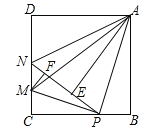
    ①△CMP∽△BPA；

    ②四边形AMCB的面积最大值为10；

    ③当P为BC中点时，AE为线段NP的中垂线；

    ④线段AM的最小值为；

    ⑤当△ABP≌△ADN时，BP=．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

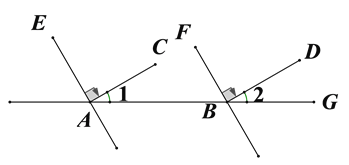
    【题目】(8分)看图填空,并在括号内注明理由依据,

    解: ∵∠1=30°, ∠2=30°

    ∴∠1=∠2

    ∴_______//________（_______________________________________）

    又AC⊥AE(已知)

    ∴∠EAC=90°（______________）

    ∴∠EAB=∠EAC+∠1=120°

    同理: ∠FBG=∠FBD+∠2=_________°.

    ∴∠EAB=∠FBG（_____________________________________）.

    ∴______________//____________(同位角相等,两直线平行)

    查看答案和解析>>

    同步练习册答案