
【题目】如图,已知二次函数![]() 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.

(1)求二次函数![]() 的解析式;
的解析式;
(2)将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,直线y=m(m>0)交
,直线y=m(m>0)交![]() 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,![]() 、
、![]() 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与![]() 、
、![]() 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与![]() 、
、![]() 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)根据待定系数法即可解决问题.
(2)先求出抛物线y2的顶点坐标,再求出其解析式,利用方程组以及根与系数关系即可求出MN.
(3)用类似(2)的方法,分别求出CD、EF即可解决问题.
试题解析:(1)∵二次函数![]() 过(﹣2,4),(﹣4,4)两点,∴
过(﹣2,4),(﹣4,4)两点,∴![]() ,解得:
,解得: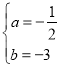 ,∴二次函数
,∴二次函数![]() 的解析式
的解析式![]() .
.
(2)∵![]() =
=![]() ,∴顶点坐标(﹣3,
,∴顶点坐标(﹣3,![]() ),∵将
),∵将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,∴抛物线
,∴抛物线![]() 的顶点坐标(﹣1,
的顶点坐标(﹣1,![]() ),∴抛物线
),∴抛物线![]() 为
为![]() ,由
,由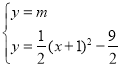 ,消去y整理得到
,消去y整理得到![]() ,设
,设![]() ,
,![]() 是它的两个根,则MN=
是它的两个根,则MN=![]() =
=![]() =
=![]() ;
;
(3)由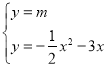 ,消去y整理得到
,消去y整理得到![]() ,设两个根为
,设两个根为![]() ,
,![]() ,则CD=
,则CD=![]() =
=![]() =
=![]() ,由
,由 ,消去y得到
,消去y得到![]() ,设两个根为
,设两个根为![]() ,
,![]() ,则EF=
,则EF=![]() =
=![]() =
=![]() ,∴EF=CD,EF∥CD,∴四边形CEFD是平行四边形.
,∴EF=CD,EF∥CD,∴四边形CEFD是平行四边形.
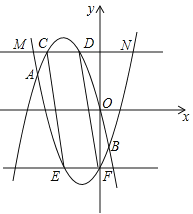


科目:初中数学 来源: 题型:
【题目】把下面的推理过程补充完整,并在括号内注明理由.
如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,

试说明:(1)∠C=∠F;(2)AC∥DF.
解:(1)∵AD=BE(已知)
∴AD+DB=DB+BE( ① )
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠( ② ) ( ③ )
又∵BC=EF(已知)
∴△ABC≌△DEF( ④ )
∴∠C=∠F,∠A=∠FDE( ⑤ )
∴AC∥DF( ⑥ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径均为![]() 个单位长度的半圆
个单位长度的半圆![]() ,
, ![]() ,
, ![]() …….组成一条平滑的曲线,点
…….组成一条平滑的曲线,点![]() 从原点
从原点![]() 出发,沿这条曲线向右运动,速度为每秒
出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第
个单位长度,则第![]() 时,点
时,点![]() 的坐标是( )
的坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com