练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】函数y=（m﹣1）x2m2﹣3是反比例函数，则m的值为

    【答案】-1
    【解析】解：∵函数y=（m﹣1）x2m2﹣3是反比例函数，
    ∴2m2﹣3=﹣1且m﹣1≠0．
    整理，得
    2（m+1）（m﹣1）=0且m﹣1≠0．
    解得 m=﹣1．
    故答案是：﹣1．
    【考点精析】本题主要考查了反比例函数的概念的相关知识点，需要掌握形如y＝k/x（k为常数，k≠0）的函数称为反比例函数．自变量x的取值范围是x不等于0的一切实数，函数的取值范围也是一切非零实数才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，二次函数y=2（x﹣1）2+3的顶点坐标是（　　）

    A. （1，3） B. （1，﹣3） C. （﹣1，3） D. （﹣1，﹣3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

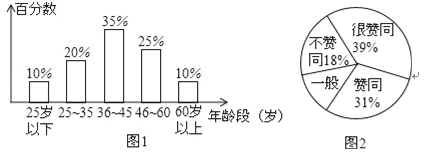
    【题目】据报载，在“百万家庭低碳行，垃圾分类要先行”活动中，某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查，并将调查结果分别绘成条形图（图1）、扇形图（图2）．

    （1）图2中所缺少的百分数是 ；

    （2）这次随机调查中，如果公民年龄的中位数是正整数，那么这个中位数所在年龄段是 ____ （填写年龄段）；

    （3）这次随机调查中，年龄段是“25岁以下”的公民中“不赞成”的有5名，它占“25岁以下”人数的百分数是 ___ ；

    （4）如果把所持态度中的“很赞同”和“赞同”统称为“支持”，那么这次被调查公民中“支持”的人有 ____名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形ABCD中，点P是对角线AC上的任意一点（不包括端点），以P为圆心的圆与AB相切，则AD与⊙P的位置关系是（　　）

    A. 相离 B. 相切 C. 相交 D. 不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题提出

    某商店经销《超能陆战队》超萌“小白”（图1）玩具，“小白”玩具每个进价60元．为进行促销，商店制定如下“优惠”方案：如果一次销售数量不超过10个，则销售单价为100元/个；如果一次销售数量超过10个，每增加一个，所有“小白”玩具销售单价降低1元/个，但单价不得低于80元/个．一次销售“小白”玩具的单价y（元/个）与销售数量x（个）之间的函数关系如图2所示．

    （1）求m的值并解释射线BC所表示的实际意义；

    （2）写出该店当一次销售x个时，所获利润w（元）与x（个）之间的函数关系式；

    （3）店长经过一段时间的销售发现：即并不是销量越大利润越大（比如，卖25个赚的钱反而比卖30个赚的钱多）．为了不出现这种现象，在其他条件不变的情况下，店长应把原来的最低单价80（元/个）至少提高到多少元/个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

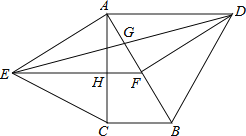
    【题目】如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：

    ①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=BD

    其中正确结论的为______（请将所有正确的序号都填上）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当x取（ ）时，代数式3（2-x）和2（3+x）的值相等。

    A. 1 B. 2 C. -2 D. 0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数过（﹣2，4），（﹣4，4）两点．

    （1）求二次函数的解析式；

    （2）将沿x轴翻折，再向右平移2个单位，得到抛物线，直线y=m（m＞0）交于M、N两点，求线段MN的长度（用含m的代数式表示）；

    （3）在（2）的条件下，、交于A、B两点，如果直线y=m与、的图象形成的封闭曲线交于C、D两点（C在左侧），直线y=﹣m与、的图象形成的封闭曲线交于E、F两点（E在左侧），求证：四边形CEFD是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为4的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的有 （写出所有正确结论的序号）

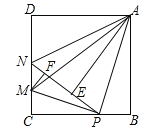
    ①△CMP∽△BPA；

    ②四边形AMCB的面积最大值为10；

    ③当P为BC中点时，AE为线段NP的中垂线；

    ④线段AM的最小值为；

    ⑤当△ABP≌△ADN时，BP=．

    查看答案和解析>>

    同步练习册答案