
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�P��BC����һ���㣨����B��C���㣩������ABP��ֱ��AP���ۣ���B���ڵ�E������CD����һ��M��ʹ�ý���CMP��ֱ��MP���ۺ�C����ֱ��PE�ϵĵ�F����ֱ��PE��CD�ڵ�N������MA��NA�������½�������ȷ���� ��д��������ȷ���۵���ţ�
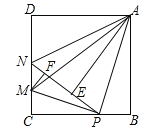
�١�CMP�ס�BPA��
���ı���AMCB��������ֵΪ10��
�۵�PΪBC�е�ʱ��AEΪ�߶�NP���д��ߣ�
���߶�AM����СֵΪ![]() ��
��
�ݵ���ABP�ա�ADNʱ��BP=![]() ��
��
���𰸡��٢ڢݣ�
��������
����������ߡ�APB=��APE����MPC=��MPN���ߡ�CPN+��NPB=180�㣬��2��NPM+2��APE=180�㣬���MPN+��APE=90�㣬���APM=90�㣬�ߡ�CPM+��APB=90�㣬��APB+��PAB=90�㣬���CPM=��PAB�����ı���ABCD�������Σ���AB=CB=DC=AD=4����C=��B=90�㣬���CMP�ס�BPA���ʢ���ȷ����PB=x����CP=4��x���ߡ�CMP�ס�BPA����![]() ����CM=
����CM=![]() x��4��x������S�ı���AMCB=
x��4��x������S�ı���AMCB=![]() [4+
[4+![]() x��4��x��]��4=
x��4��x��]��4=![]() =
=![]() ����x=2ʱ���ı���AMCB������ֵΪ10���ʢ���ȷ����PB=PC=PE=2ʱ����ND=NE=y����RT��PCN�У�
����x=2ʱ���ı���AMCB������ֵΪ10���ʢ���ȷ����PB=PC=PE=2ʱ����ND=NE=y����RT��PCN�У�![]() ���
���![]() ����NE��EP���ʢ۴�����MG��AB��G����AM=
����NE��EP���ʢ۴�����MG��AB��G����AM=![]() =
=![]() ����AG��СʱAM��С����AG=AB��BG=AB��CM=4��
����AG��СʱAM��С����AG=AB��BG=AB��CM=4��![]() x��4��x��=
x��4��x��=![]() ����x=1ʱ��AG��Сֵ=3����AM����Сֵ=
����x=1ʱ��AG��Сֵ=3����AM����Сֵ=![]() =5���ʢܴ���
=5���ʢܴ���
�ߡ�ABP�ա�ADNʱ�����PAB=��DAN=22.5�㣬��AB��ȡһ��Kʹ��AK=PK����PB=z�����KPA=��KAP=22.5�㣮�ߡ�PKB=��KPA+��KAP=45�㣬���BPK=��BKP=45�㣬��PB=BK=z��AK=PK=![]() z����z+
z����z+![]() z=4����z=
z=4����z=![]() ����PB=
����PB=![]() �ʢ���ȷ��
�ʢ���ȷ��
�ʴ�Ϊ���٢ڢݣ�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ڡ�ABC�У�����ABC������a,b,c���� a:b: c=5:12:13���жϡ�ABC����״.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ǽ���Ϲ̶�һ����ŵ�ľ������������Ҫ�� ��ö���ӣ�
A. l B. 2 C. 3 D. ������ö
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y=��x��3��2��4��ͼ�������н��ۣ��ٿ������ϣ��ڶԳ�����ֱ��x=��3���۶��������ǣ���3����4��������x�����������㣮������ȷ�Ľ����ǣ�������
A. �٢� B. �٢� C. �ڢ� D. �ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯ѧ���鷨�������Բ�����Ʒ��A��B��C��D�ĸ��ȼ������������������ȡ����ѧ���鷨��Ʒ������������з���������������ͳ��ͼ������ͳ��ͼ���£�

����������Ϣ����������⣺
��1������γ�ȡ��������������
��2������ͼ���а�����ͳ��ͼ����������
��3����֪��У��λ���յ�������Ʒ750�ݣ�������Ʋ�����Ʒ�ﵽB�����ϣ���A����B�����ж��ٷݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��m��n���ڵڶ����ޣ����Q��n��m���ڣ�������
A.��һ����B.�ڶ�����C.��������D.��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com