
【题目】把下面的推理过程补充完整,并在括号内注明理由.
如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,

试说明:(1)∠C=∠F;(2)AC∥DF.
解:(1)∵AD=BE(已知)
∴AD+DB=DB+BE( ① )
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠( ② ) ( ③ )
又∵BC=EF(已知)
∴△ABC≌△DEF( ④ )
∴∠C=∠F,∠A=∠FDE( ⑤ )
∴AC∥DF( ⑥ )
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=2(x﹣1)2+3的顶点坐标是( )
A. (1,3) B. (1,﹣3) C. (﹣1,3) D. (﹣1,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
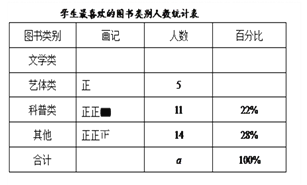
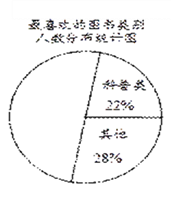

请结合图中的信息解答下列问题:
(1)随机抽取的样本容量a为 ;
(2)补全扇形统计图和条形统计图;
(3)已知该校有600名学生,估计全校最喜欢文学类图书的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
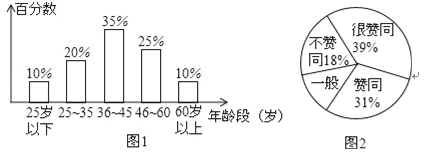
【题目】据报载,在“百万家庭低碳行,垃圾分类要先行”活动中,某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
(1)图2中所缺少的百分数是 ;
(2)这次随机调查中,如果公民年龄的中位数是正整数,那么这个中位数所在年龄段是 ____ (填写年龄段);
(3)这次随机调查中,年龄段是“25岁以下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是 ___ ;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有 ____名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点P是对角线AC上的任意一点(不包括端点),以P为圆心的圆与AB相切,则AD与⊙P的位置关系是( )
A. 相离 B. 相切 C. 相交 D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.

(1)求二次函数![]() 的解析式;
的解析式;
(2)将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,直线y=m(m>0)交
,直线y=m(m>0)交![]() 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,![]() 、
、![]() 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与![]() 、
、![]() 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与![]() 、
、![]() 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com