
【题目】解方程:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() +1=
+1=![]() .
.
【答案】(1)x=4;(2) x=![]() ;(3) 原分式方程无解
;(3) 原分式方程无解
【解析】
(1)方程两边都乘以(x+2)(x-2),去分母,再化简求值;
(2)方程两边都乘以(x+1)(x-1),去分母,再化简求值;
(2)方程两边都乘以(x+1)(x-1),去分母,再化简求值,注意检验.
方程两边乘(x+2)(x-2),得3x(x-2)+2(x+2)=3(x+2)(x-2),
化简得-4x=-16,
解得x=4.
经检验,x=4是原方程的解.
所以原方程的解是x=4.
(2)方程两边都乘以(x+1)(x-1),去分母,得4-(x+1)(x+2)=-(x+1)(x-1).
解得x=![]() .
.
经检验,x=![]() 是原方程的解.
是原方程的解.
所以原方程的解是x=![]() .
.
(3)方程两边同时乘以(x+1)(x-1),得:
4+x2-1=x2-2x+1,
解得:x=-1,
检验:x=-1时,(x+1)(x-1)=0,所以x=-1是增根,原分式方程无解.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】△ABC和△A′B′C′在平面直角坐标系中的位置分别如图所示.
(1)分别写出下列各点的坐标:A_______;B_______;C_______;
(2)△ABC由△A′B′C′经过怎样的平移得到?
答:_____________________________________
(3)求△ABC面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
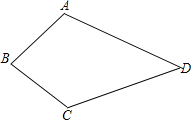
【题目】(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
(B类)已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2 , 若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题:
(1)已知,如图1,△ABC中,P点是∠ABC和∠ACB的角平分线的交点,求证:∠P=![]() ∠A+90°。
∠A+90°。
(2)如图2,若P点是∠ABC和∠ACB外角的角平分线的交点,∠A=80°,那么∠P=____°;
(3)如图3,△ABC中,若P点是∠ABC外角和∠ACB外角的角平分线的交点,∠A=![]() ,那么∠P=________(请用含
,那么∠P=________(请用含![]() 的代数式表示)
的代数式表示)



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com