练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知一个三角形的三边长分别为5、7、8，则其内切圆的半径为（ ）
    A.
    B.
    C.
    D.

    【答案】C
    【解析】如图，AB=7，BC=5，AC=8，内切圆的半径为r，切点为D、E、F，作AD⊥BC于D，设BD=x，则CD=5﹣x．

    由勾股定理可知：AD2=AB2﹣BD2=AC2﹣CD2，

    即72﹣x2=82﹣（5﹣x）2，解得x=1，

    ∴AD=4 ，

    ∵ BCAD= （AB+BC+AC）r，

    ×5×4 = ×20×r，

    ∴r= ，

    故答案为：C

    面积法求内切圆半径：先利用勾股定理列出方程求BC边上的高，进而求出三角形面积，三角形的面积还可以等于三个以O为顶点，各边为边的小三角形的面积和，从而建立以r 为未知数的简单的方程，求出r.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图①，(1)∠AOB＝60°，∠BOC＝36°OD平分∠BOC，OE平分∠AOC，则∠EOD＝____度；

    （2）若∠AOB＝90°，OD平分∠BOC，OE平分∠AOC，则∠EOD＝__________;

    （3）若∠AOB＝α，其它条件同（2），则∠EOD＝_________________.

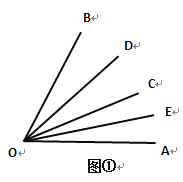
    类比应用：

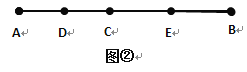
    如图②，已知线段AB，C是线段AB上任一点，D、E分别是AC、CB的中点，试猜想DE与AB的数量关系为_____________，并写出求解过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰Rt△ABC中，∠ABC=90°，AB=CB=2，点D为AC的中点，点E，F分别是线段AB，CB上的动点，且∠EDF=90°，若ED的长为m，则△BEF的周长是（用含m的代数式表示）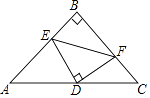

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,∠1+∠2=180°,∠B=∠3.

    (1)判断DE与BC的位置关系,并说明理由:

    解:结论:______________.

    理由:∵∠1+∠2=180°,

    ∴_________________

    ∴∠ADE=∠3,

    ∵∠B=∠3

    ∴______________

    ∴DE∥BC;

    (2)若∠C=65°，求∠DEC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】去冬今春，某市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．
    （1）求饮用水和蔬菜各有多少件？
    （2）现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，l1表示某公司一种产品一天的销售收入与销售量的关系，l2表示该公司这种产品一天的销售成本与销售量的关系．

    （1）x＝1时，销售收入＝　 　万元，销售成本＝　 　万元，盈利（收入﹣成本）＝　 　万元；

    （2）一天销售　 　件时，销售收入等于销售成本；

    （3）l2对应的函数表达式是　 　；

    （4）你能写出利润与销售量间的函数表达式吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司共有A，B，C三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
    各部门人数及每人所创年利润统计表

    部门

    员工人数

    每人所创的年利润/万元

    A

    5

    10

    B

    b

    8

    C

    c

    5


    （1）①在扇形图中，C部门所对应的圆心角的度数为
    ②在统计表中，b= ， c=
    （2）求这个公司平均每人所创年利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知BC=EC，∠BCE=∠ACD，如果只添加一个条件，使△ABC ≌ △DEC，则添加的条件不能为（ ）

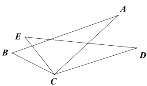
    A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD.

    （1）求证：四边形OCED是菱形；

    （2）若AB＝3，BC＝4，求四边形OCED的面积．

    查看答案和解析>>

    同步练习册答案