
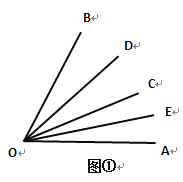
【题目】如图①,(1)∠AOB=60°,∠BOC=36°OD平分∠BOC,OE平分∠AOC,则∠EOD=____度;
(2)若∠AOB=90°,OD平分∠BOC,OE平分∠AOC,则∠EOD=__________;
(3)若∠AOB=α,其它条件同(2),则∠EOD=_________________.
类比应用:
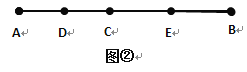
如图②,已知线段AB,C是线段AB上任一点,D、E分别是AC、CB的中点,试猜想DE与AB的数量关系为_____________,并写出求解过程.
【答案】(1)30;(2)45度;(3)![]() α;类比应用:DE=
α;类比应用:DE=![]() AB,见解析.
AB,见解析.
【解析】
(1)根据角平分线的定义,∠COD=![]() ∠BOC,∠COE=
∠BOC,∠COE=![]() ∠AOC,所以∠EOD=
∠AOC,所以∠EOD=![]() ∠AOB,代入数据计算即可;
∠AOB,代入数据计算即可;
(2)与(1)的求解与解答思路相同;
(3)与(1)的求解与解答思路相同;
类比应用:把题中的∠AOB换成线段AB,相应的角平分线换成中点即可.
解:(1)∵∠AOB=60°,∠BOC=36°
∴∠AOC=24°
∵OD平分∠BOC,OE平分∠AOC,
∴∠DOC=![]() ∠BOC=18°,∠COE=
∠BOC=18°,∠COE=![]() ∠AOC=12°,
∠AOC=12°,
∴∠EOD=∠DOC+∠COE=![]() ∠BOC+
∠BOC+![]() ∠AOC=
∠AOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB,
∠AOB,
∵∠AOB=60°,
∴∠EOD=![]() ×60°=30°;
×60°=30°;
(2)同理∠EOD=![]() ∠AOB=
∠AOB=![]() ×90°=45°;
×90°=45°;
(3)同理∠EOD=![]() ∠AOB=
∠AOB=![]() ;
;
类比应用:如图②,∵D是AC的中点,E是BC的中点,
∴DC=![]() AC,EC=
AC,EC=![]() BC;
BC;
∴DE=![]() AC+
AC+![]() BC=
BC=![]() (AC+BC)=
(AC+BC)=![]() AB.
AB.
故答案为:(1)30;(2)45度;(3)![]() α;类比应用:DE=
α;类比应用:DE=![]() AB,见解析.
AB,见解析.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】某乒乓球馆有两种计费方案,如下图表.李强和同学们打算周末去此乒乓球馆连续打球4小时,经服务生测算后,告知他们包场计费方案会比人数计费方案便宜,则他们参与包场的人数至少为( )
包场计费:包场每场每小时50元,每人须另付入场费5元 |
人数计费:每人打球2小时20元,接着续打球每人每小时6元 |
A. 9B. 8C. 7D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
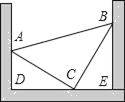
【题目】如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.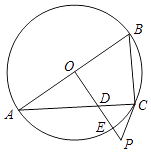
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M,N分别在BC,AC上,且BM=CN现有以下四个结论:
①DN=DM; ② ∠NDM=90°; ③ 四边形CMDN的面积为4; ④△CMN的面积最大为2.
其中正确的结论有( )
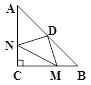
A. ①②④; B. ①②③; C. ②③④; D. ①②③④.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com