
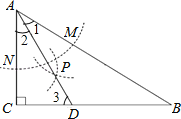
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
【答案】A
【解析】
试题分析:①根据作图的过程可以判定AD是∠BAC的角平分线;
②利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;
③利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上;
④根据直角三角形的性质得出AD=2CD,再由线段垂直平分线的性质得出AD=BD,进而可得出结论.
解:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°﹣∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
∵∠2=30°,
∴AD=2CD.
∵点D在AB的中垂线上,
∴AD=BD,
∴BD=2CD.
故④正确.
故选A.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】将数轴按如图所示从点A开始折出一等边△ABC,设A表示的数为x-3, B表示的数为2x-5,C表示的数为5-x,则x=_______.将△ABC向右滚动,则点2016与点_____重合.(填A.B.C)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程:①3x﹣1=2x+1,②![]() ,③
,③![]() ,④
,④![]() x﹣1=x中,解为x=2的是方程( )
x﹣1=x中,解为x=2的是方程( )
A. ①、②和③ B. ①、③和④ C. ②、③和④ D. ①、②和④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形纸片,剪下一个正方形,剩下一个长方形,称为第一次操作;在剩下的长方形纸片中再剪下一个正方形,剩下一个长方形,称为第二次操作;…;若在第n次操作后,剩下的长方形为正方形,则称原长方形为n阶奇异长方形.如图1,长方形ABCD中,若AB=2,BC=6,则称长方形ABCD为2阶奇异长方形.

(1)判断与操作:如图2,长方形ABCD长为10,宽为6,它是奇异长方形,请写出它是____阶奇异长方
形,并在图中画出裁剪线;
探究与计算:已知长方形ABCD的一边长为24,另一边长为a (a<24),且它是3阶奇异长方形,请画出所
有可能的长方形ABCD及裁剪线的示意图,并求出相应的a值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x (元)的一次函数.
(1)直接写出y与x之间的函数关系式y=
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求 ![]() 的值.
的值.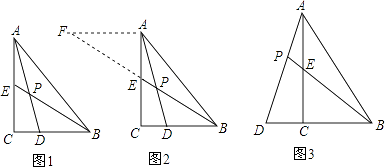
(1)小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
请回答: ![]() 的值为 .
的值为 .
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.
①求 ![]() 的值;
的值;
(3)②若CD=2,则BP= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境、低碳出行已渐渐成为人们的习惯.最近无为县城又引进了共享单车,只需要交点押金,就可以通过扫描二维码的方式解锁一辆停在路边的自行车,以极低的费用,轻松骑到目的地.王老师家与学校相距2km,现在每天骑共享单车到学校所花的时间比过去骑电动车多用4min.已知王老师骑电动车的速度是骑共享单车速度的1.5倍,则王老师骑共享单车的速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com