
【题目】在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M,N分别在BC,AC上,且BM=CN现有以下四个结论:
①DN=DM; ② ∠NDM=90°; ③ 四边形CMDN的面积为4; ④△CMN的面积最大为2.
其中正确的结论有( )
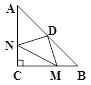
A. ①②④; B. ①②③; C. ②③④; D. ①②③④.
【答案】D
【解析】连接CD,
∵在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,
∴∠B=∠NCD=45°,CD=BD,∠CDB=90°,S△CDB=![]() S△ABC=
S△ABC=![]() ·
·![]() AC·BC=
AC·BC=![]() =4 ,
=4 ,
又∵BM=CN,
∴△DBM≌△DCN,
∴DN=DM,∠CDN=∠DBM,S△CDN=S△DBM,
∴∠DMN=∠CDN+∠CDM=∠CDM+∠BDM=∠CDB=90°,
S四边形CMDN=S△CDN+S△CDM= S△BDM+S△CDM=S△CBD=4.
∵S△CMN+S△DMN= S四边形CMDN=4,
∴当S△DMN最小时,S△CMN的面积最大,
∴当DM⊥BC时,DM=DN=2,此时S△DMN最小=2,
∴此时,S△CMN的面积最大=4-2=2.
综上所述,上述四个结论全都正确.
故选D.


科目:初中数学 来源: 题型:
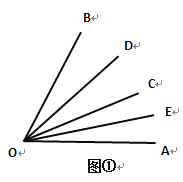
【题目】如图①,(1)∠AOB=60°,∠BOC=36°OD平分∠BOC,OE平分∠AOC,则∠EOD=____度;
(2)若∠AOB=90°,OD平分∠BOC,OE平分∠AOC,则∠EOD=__________;
(3)若∠AOB=α,其它条件同(2),则∠EOD=_________________.
类比应用:
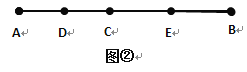
如图②,已知线段AB,C是线段AB上任一点,D、E分别是AC、CB的中点,试猜想DE与AB的数量关系为_____________,并写出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(﹣3,1),点A的坐标为(2,0),点B的坐标为(1,﹣ ![]() ),点D在x轴上,且点D在点A的右侧.
),点D在x轴上,且点D在点A的右侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,菱形ABCD沿x轴向左以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与AD相切,且切点为AD的中点时,连接AC,求t的值及∠MAC的度数;
(3)在(2)的条件下,当点M与AC所在的直线的距离为1时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
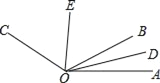
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.

(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)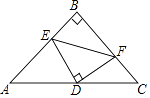
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠B=∠3.

(1)判断DE与BC的位置关系,并说明理由:
解:结论:______________.
理由:∵∠1+∠2=180°,
∴_________________
∴∠ADE=∠3,
∵∠B=∠3
∴______________
∴DE∥BC;
(2)若∠C=65°,求∠DEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
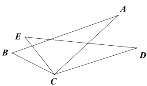
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com