
����Ŀ����ͼ����M������ABCD��ƽ��ֱ������ϵ�У���M������Ϊ����3��1������A������Ϊ��2��0������B������Ϊ��1���� ![]() ������D��x���ϣ��ҵ�D�ڵ�A���Ҳ࣮
������D��x���ϣ��ҵ�D�ڵ�A���Ҳ࣮
��1��������ABCD���ܳ���
��2������M��x��������ÿ��2����λ���ȵ��ٶ�ƽ�ƣ�����ABCD��x��������ÿ��3����λ���ȵ��ٶ�ƽ�ƣ��������ƶ���ʱ��Ϊt���룩������M��AD���У����е�ΪAD���е�ʱ������AC����t��ֵ����MAC�Ķ�����
��3���ڣ�2���������£�����M��AC���ڵ�ֱ�ߵľ���Ϊ1ʱ����t��ֵ��
���𰸡�
��1���⣺����B��BE��AD������ΪE��
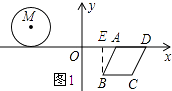
��B��1���� ![]() ����A��2��0����
����A��2��0����
��BE= ![]() ��AE=1��
��AE=1��
��AB= ![]() =2��
=2��
���ı���ABCDΪ���Σ�
��AB=BC=CD=AD��
�����ε��ܳ�=2��4=8��
��2���⣺��ͼ2��ʾ����M��x�������ΪF��AD���е�ΪE��
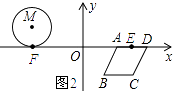
��M����3��1����
��F����3��0����
��AD=2����EΪAD���е㣬
��E��3��0����
��EF=6��
��2t+3t=6��
��ã�t= ![]() ��
��
ƽ�Ƶ�ͼ����ͼ3��ʾ������B��BE��AD������ΪE������MF��FΪ��M��AD���е㣮
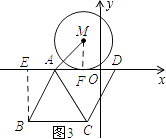
���ɣ�1����֪��AE=1��BE= ![]() ��
��
��tan��EAB= ![]() ��
��
���EAB=60�㣮
���FAB=120�㣮
���ı���ABCD�����Σ�
���FAC= ![]() ��FAB=
��FAB= ![]() ��120��=60�㣮
��120��=60�㣮
��ADΪ��M�����ߣ�
��MF��AD��
��FΪAD���е㣬
��AF=MF=1��
���AFMΪ����ֱ�������Σ�
���MAF=45�㣮
���MAC=��MAF+��FAC=45��+60��=105�㣮
��3���⣺��ͼ4��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE��
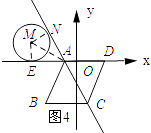
���ı���ABCDΪ���Σ���DAB=120�㣬
���DAC=60�㣮
��AC��AD��ԲM�����ߣ�
���MAE=30�㣮
��ME=MN=1��
��EA= ![]() ��
��
��3t+2t=5�� ![]() ��
��
��t=1�� ![]() ��
��
��ͼ5��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE��
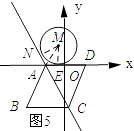
���ı���ABCDΪ���Σ���DAB=120�㣬
���DAC=60�㣮
���NAE=120�㣮
��AC��AD��ԲM�����ߣ�
���MAE=60�㣮
��ME=MN=1��
��EA= ![]() ��
��
��3t+2t=5+ ![]() ��
��
��t=1+ ![]() ��
��
����������t=1�� ![]() ��t=1+
��t=1+ ![]() ʱ��ԲM��AC���У�
ʱ��ԲM��AC���У�
����������1������B��BE��AD������ΪE����A��B��������ɶ��������AB�ij��������ɵ�����ABCD���ܳ���
��2�����M��x�������ΪF��AD���е�ΪE.�������������EF�ij����Ӷ����t��ֵ������B��BE��AD������ΪE������MF��FΪ��M��AD���е㣮����AD��ԲM�����ߺ����ε����ʣ���֤�á�AFMΪ����ֱ�������Σ��Ӷ���á�MAC�Ķ�����
��3����ͼ4��ͼ5�У�����AM��������MN��AC������ΪN����ME��AD������ΪE��ͼ4�У����ı���ABCDΪ���Σ��ɵá�DAC=60�㣬����AC��AD��ԲM�����ߣ��ɵá�MAE=30�㣬�����Ǻ����ɵ�EA�ij�������3t+2t=5-AE�����t��ֵ��ͼ5�У�ͬ�������AEden��������3t+2t=5+AE���t��ֵ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ��IJ���ʽ��ʾ���в��ȹ�ϵ��
��1��x��ȥ6����12��
��2��x��2����5�IJ��Ǹ�����
��3��x��3����4�ĺ��ǷǸ�����
��4��y��5����9�IJ����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ������С�������ɽ������ɽ������ɽ���Ĺ���������;��Ϣ��һ��ʱ����������ɽ�ų��������õ�ʱ��Ϊt�������������ߵ�·��Ϊs��������s��t֮��ĺ�����ϵ��ͼ��ʾ������˵������������ ��

A��С����;��Ϣ����20����
B��С����Ϣǰ��ɽ��ƽ���ٶ�Ϊÿ����70��
C��С�����������������ߵ�·��Ϊ6600��
D��С����Ϣǰ��ɽ��ƽ���ٶȴ�����Ϣ����ɽ��ƽ���ٶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
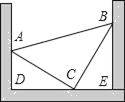
����Ŀ����ͼ����һ�����ֱ�����������(��ABC�����С�ACB��90��)��������һ�����ڣ���������A��B��C�ֱ����ڰ����ڱ��ϣ���֪��ADE����BED��90�㣬���AD��5cm��BE��7cm���������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������O����OP��AB������AC�ڵ�D������O�ڵ�E����ʹ��PCA=��ABC��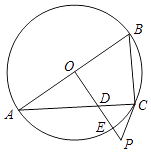
��1����֤��PC�ǡ�O�����ߣ�
��2������P=60�㣬PC=2����PE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=8��BC=6����E�ڱ�AB�ϣ���F�ڱ�CD�ϣ���G��H�ڶԽ���AC�ϣ����ı���EGFH�����Σ���AE�ij��ǣ� ��
A.2 ![]()
B.3 ![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
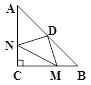
����Ŀ������ABC�У���ACB=90����AC=BC=4����DΪAB���е㣬M��N�ֱ���BC��AC�ϣ���BM=CN���������ĸ����ۣ�
��DN=DM�� �� ��NDM=90���� �� �ı���CMDN�����Ϊ4�� �ܡ�CMN��������Ϊ2.
������ȷ�Ľ����У� ��
A. �٢ڢ��� B. �٢ڢ��� C. �ڢۢ��� D. �٢ڢۢ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����վ��ij��˾���˵ļ��ֻ���1530�֣����ֻ���1150�֣��ּƻ���50��A��B�����ͺŵij��Ὣ��������������������֪���ֻ���35�ֺ����ֻ���15�ֿ�װ��һ��A�ͻ���������25�ֺ����ֻ���35�ֿ�װ��һ��B�ͻ���������Ҫ����A��B���ֻ���Ľ����������ļ��ַ���?������Ƴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��m��ֱ��n��ֱ�ཻ��O����A��ֱ��m���˶�����B ��ֱ��n���˶���AC��BC�ֱ��ǡ�BAO�͡�ABO�Ľ�ƽ���ߣ�
��1�����ACB�Ĵ�С��
��2����ͼ2����BD����AOB����ǡ�OBE�Ľ�ƽ���ߣ�BD��AC�ཻ�ڵ�D����A��B���˶��Ĺ����У���ADB�Ĵ�С�Ƿ�ᷢ���仯���������仯����˵�����ɣ����������仯���������ֵ��
��3����ͼ3����C��ֱ����AB����F���������AGO����BCF=45������֤��CF��OB��
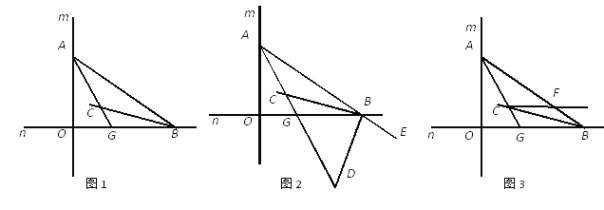
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com